
题目列表(包括答案和解析)
1.对条件理解错误,从而导致判断错误;
2.考查充分条件、必要条件在集合、函数、不等式方面的应用如例2.
[典例精析]
例1(2005•湖北)对任意实数a,b,c,给出下列命题:
①“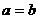 ”是“
”是“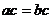 ”充要条件;
”充要条件;
②“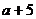 是无理数”是“a是无理数”的充要条件
是无理数”是“a是无理数”的充要条件
③“a>b”是“a2>b2”的充分条件;
④“a<5”是“a<3”的必要条件.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
解析:容易判断②,④是正确的.若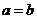 ,则
,则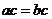 ;反之,若
;反之,若
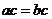 则
则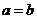 或
或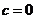 ,所以“
,所以“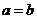 ”是“
”是“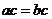 ”的充分条件而不是必要条件,①是假命题,
”的充分条件而不是必要条件,①是假命题, 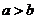 时不一定有
时不一定有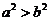 因为由ac=bc推不出a=b;所以③是假命题;
因为由ac=bc推不出a=b;所以③是假命题;
答案: B.
例2(2005•湖南)集合A={x|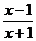 <0=,B={x
|| x -b|<a
<0=,B={x
|| x -b|<a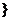 ,若“a=1”是“A∩B≠
,若“a=1”是“A∩B≠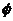 ”的充分条件,则b的取值范围是( )
”的充分条件,则b的取值范围是( )
A.-2≤b<0 B.0<b≤2 C.-3<b<-1 D.-1≤b<2
解析:由题意得:A:-1<x<1,B:b-a<x<a+b.由”a=1”是“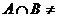 ¢”的充分条件.
¢”的充分条件.
则A:-1<x<1与B: b-1<x<1+b交集不为空.所以-2<b<2.检验知: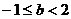 能使
能使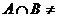 ¢.
¢.
答案: D.
例3. (2005•北京)“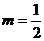 ”是“直线
”是“直线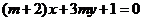 与直线
与直线
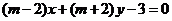 相互垂直”的( )
相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
解析:当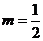 时两直线斜率乘积为
时两直线斜率乘积为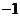 从而可得两直线垂直,当
从而可得两直线垂直,当 时两直线一条斜率为0一条;斜率不存在,但两直线仍然垂直.因此
时两直线一条斜率为0一条;斜率不存在,但两直线仍然垂直.因此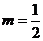 是题目中给出的两条直线垂直的充分但不必要条件.
是题目中给出的两条直线垂直的充分但不必要条件.
答案:B.
[常见误区]
1.充分条件、必要条件的判断及证明;如例1,例3.
1.掌握充分条件、必要条件及充要条件的意义.
1.3 充分必要条件
[考点透视]
9.已知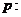 方程
方程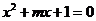 有两个不相等的负实根;
有两个不相等的负实根;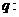 方程
方程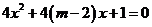 无
无
实根.若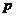 或
或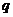 为真,
为真,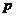 且
且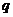 为假,求
为假,求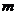 的取值范围.
的取值范围.
8.下列三个方程中,至少有一个方程有实数解,求实数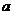 的取值范围.
的取值范围.
(1) 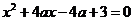 ; (2)
; (2) 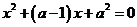 ;
;
(3)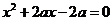 .
.
7.判断命题的真假:二次函数
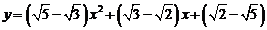 的图象与
的图象与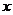 轴相
轴相
交,且二次函数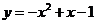 的图象与
的图象与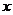 轴相交.
轴相交.
6.把下面不完整的命题补充完整,并使之成为真命题.
若函数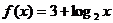 的图象与
的图象与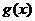 的图象关于
对称,则函数
的图象关于
对称,则函数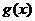 =
=
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
5.命题“若a>b,则2a>2b-1”的否命题为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com