
题目列表(包括答案和解析)
2.不能准确把握子集、真子集、相等、补集等相关概念,在转化命题时往往出现错误;
1.解题粗心大意,不考虑元素的特征,对数集,点集理解有误;如
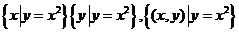 就表示完全不同的三个集合,如不注意它们的区别,很容易出错.
就表示完全不同的三个集合,如不注意它们的区别,很容易出错.
2.对集合语言和集合思想的运用,如方程与不等式的解集,函数的定义域和值域.如例2.
[典例精析]
例1:(2005·浙江)设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记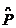 ={n∈N|f(n)∈P},
={n∈N|f(n)∈P},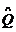 ={n∈N|f(n)∈Q},则(
={n∈N|f(n)∈Q},则(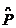 ∩
∩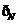
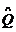 )∪(
)∪(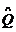 ∩
∩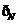
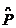 )=(
)
)=(
)
A.{0,3} B.{1,2} .C. (3,4,5) D.{1,2,6,7}
解析: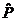 ={0,1,2},
={0,1,2},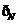
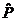 ={n∈N|n≥2},
={n∈N|n≥2},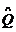 ={1,2,3},
={1,2,3},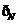
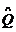 ={n∈N|n=0或n≥4},
={n∈N|n=0或n≥4},
故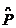 ∩
∩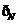
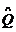 ={0},
={0},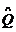 ∩
∩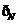
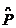 ={3},得(
={3},得(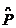 ∩
∩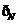
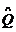 )∪(
)∪(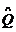 ∩
∩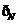
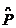 )={0,3},
)={0,3},
答案:A.
例2:(2005•上海)已知集合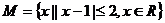 ,
,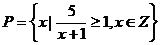 ,则
,则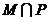 等于( )
等于( )
A.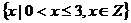 B.
B.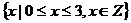
C.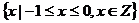 D.
D.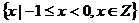
解析: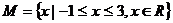 ,
, 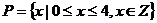
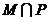 =
=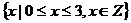 .
.
D:B.
例3:设全集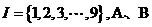 是I 的子集,若
是I 的子集,若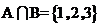 ,就称集对( A, B)为好集,那么所有好集的个数为( ).
,就称集对( A, B)为好集,那么所有好集的个数为( ).
A.6! B.
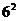 C.
C.
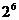 D.
D.
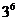
解析:要使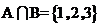 ,必须满足集合A,B 中都含有元素1,2,3, 且对全集中的其它6个元素4,5,6,7,8,9中的每个元素,要么在集合A中,要么在集合B中或不在集合A、B中,这三种情况只能选其一,于是这6个元素所处集合的不同情况为
,必须满足集合A,B 中都含有元素1,2,3, 且对全集中的其它6个元素4,5,6,7,8,9中的每个元素,要么在集合A中,要么在集合B中或不在集合A、B中,这三种情况只能选其一,于是这6个元素所处集合的不同情况为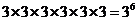 .而这6个元素所处不同集合的个数即为好集的不同个数.
.而这6个元素所处不同集合的个数即为好集的不同个数.
答案:D.
[常见误区]
1.集合的基本概念和关系、集合之间的运算是近几年的的高考热点.是每年高考必考内容之一. 如例1,例3.
2.掌握有关的术语和符号,并会用它们正确表示一些简单的集合.
1.理解集合、子集、补集、交集、并集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.
13、已知集合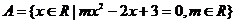 ,若A中元素至多只有一个,求
,若A中元素至多只有一个,求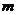 的取值范围。
的取值范围。
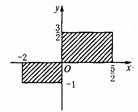
12.用适当的方法表示下图中的阴影部分的点(含边界上的点)组成的集合M。
11.已知集合M=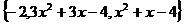 ,若
,若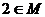 ,求满足条件的实数
,求满足条件的实数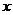 组成的集合。
组成的集合。
10.已知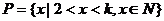 ,若集合P中恰有3个元素,求
,若集合P中恰有3个元素,求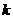 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com