
题目列表(包括答案和解析)
7.已知函数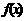 满足
满足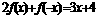 ,则
,则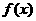 =
。
=
。
6.已知函数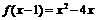 ,求函数
,求函数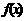 ,
,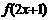 的解析式
的解析式
5.求下列函数的值域:
⑴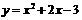
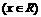 ⑵
⑵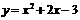
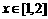
(3)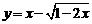 (4)
(4)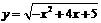
4.函数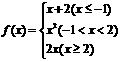 ,若
,若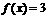 ,则
,则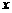 =
=
3.若函数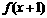 的定义域为
的定义域为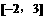 ,则函数
,则函数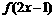 的定义域是
的定义域是
2.设函数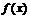 的定义域为
的定义域为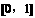 ,则函数
,则函数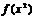 的定义域为_ _
的定义域为_ _
1.求下列函数的定义域:
⑴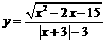 ⑵
⑵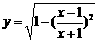
10.函数最大(小)值(定义见课本p36页)
1 利用二次函数的性质(配方法)求函数的最大(小)值
2 利用图象求函数的最大(小)值
3 利用函数单调性的判断函数的最大(小)值:
如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减则函数y=f(x)在x=b处有最大值f(b);
如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b);
例题:
9、函数的解析表达式
(1).函数的解析式是函数的一种表示方法,要求两个变量之间的函数关系时,一是要求出它们之间的对应法则,二是要求出函数的定义域.
(2)求函数的解析式的主要方法有:
1) 凑配法
2) 待定系数法
3) 换元法
4) 消参法
8.函数的奇偶性(整体性质)
(1)偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
(2).奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.
(3)具有奇偶性的函数的图象的特征
偶函数的图象关于y轴对称;奇函数的图象关于原点对称.
利用定义判断函数奇偶性的步骤:
1首先确定函数的定义域,并判断其是否关于原点对称;
2确定f(-x)与f(x)的关系;
3作出相应结论:若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数.
注意:函数定义域关于原点对称是函数具有奇偶性的必要条件.首先看函数的定义域是否关于原点对称,若不对称则函数是非奇非偶函数.若对称,(1)再根据定义判定; (2)由 f(-x)±f(x)=0或f(x)/f(-x)=±1来判定; (3)利用定理,或借助函数的图象判定 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com