
题目列表(包括答案和解析)
7.一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF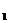 (F
(F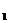 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
A.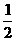 B.
B.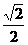 C.
C.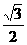 D.
D.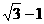
6.若椭圆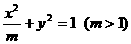 与双曲线
与双曲线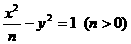 有相同的焦点F1、F2,P是两曲线的一个交点,则
有相同的焦点F1、F2,P是两曲线的一个交点,则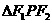 的面积是 ( )
的面积是 ( )
A.4 B.2 C.1 D.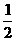
5.抛物线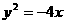 上有一点P,P到椭圆
上有一点P,P到椭圆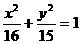 的左顶点的距离的最小值为( )
的左顶点的距离的最小值为( )
A.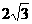 B.2+
B.2+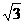 C.
C.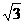 D.
D.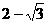
4.若抛物线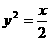 与圆
与圆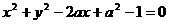 有且只有三个公共点,则
有且只有三个公共点,则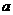 的取值范围是 ( )
的取值范围是 ( )
A.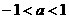 B.
B.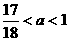 C.
C.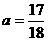 D.
D.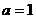
3.与曲线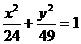 共焦点,而与曲线
共焦点,而与曲线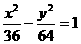 共渐近线的双曲线方程为 ( )
共渐近线的双曲线方程为 ( )
A.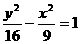 B.
B.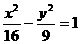
C.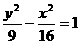 D.
D.
2.圆C切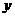 轴于点M且过抛物线
轴于点M且过抛物线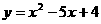 与
与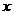 轴的两个交点,O为原点,则OM的长是 ( )
轴的两个交点,O为原点,则OM的长是 ( )
A.4 B.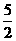 C.
C.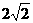 D.2
D.2
1.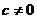 是方程
是方程 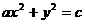 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
20.(本小题满分10分)某企业要设计一个下部是圆柱形,上部是半球形的密闭容器,容积
为常量V,问当圆柱的底面半径与圆柱的高为何值时,制造这个密闭容器的用料最省(即
容器的表面积最小).
高中学生学科素质训练
19.(本小题满分10分)已知直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B. M、N分
别为A1B1、AB的中点.
①求证:平面AMC1//平面NB1C;
②求A1B与B1C所成的角的大小;
③若A1C1=AA1=1,∠A1C1B1=90°求三棱柱ABC-A1B1C1的体积.
18.(本小题满分10分)已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC内
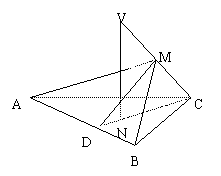 的射影,且在△ABC的高CD上,AB=a,VC与AB之间的距离为h,点M∈VC.
的射影,且在△ABC的高CD上,AB=a,VC与AB之间的距离为h,点M∈VC.
①证明:∠MDC是二面角M-AB-C的平面角;
②当∠MDC=∠CVN时,证明:VC⊥平面AMB;
③若∠MDC=∠CVN=θ.(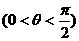 ,
,
求四面体MABC的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com