
题目列表(包括答案和解析)
16.
15.
12.__________ 13._________ 14.___________
9.________________________ 10.____________ 11.___________
5.___________ 6.__________ 7._____________ 8.____________
1.___________ 2.__________ 3._____________ 4.____________
4.等比数列{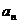 }的前
}的前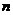 项和为
项和为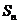 ,已知对任意的
,已知对任意的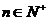 ,点
,点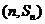 均在函数
均在函数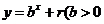 且
且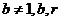 均为常数)的图像上.
均为常数)的图像上.
(1)求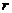 的值;
的值;
(2)当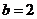 时,记
时,记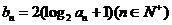 ,证明:对任意的
,证明:对任意的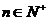 ,不等式
,不等式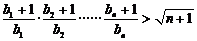 成立.
成立.
 2010-2011学年(下) 阶段测试试卷答案纸
2010-2011学年(下) 阶段测试试卷答案纸
数学试题(正卷)
3. 2009年芬兰国际象棋比赛的决赛在中国队的卜祥志和乌克兰队的科罗波夫两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,根据以往经验,每局中国队赢的概率为
2009年芬兰国际象棋比赛的决赛在中国队的卜祥志和乌克兰队的科罗波夫两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,根据以往经验,每局中国队赢的概率为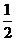 ,乌克兰队赢的概率为
,乌克兰队赢的概率为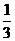 ,且每局比赛输赢互不影响.若中国队第n局的得分记为
,且每局比赛输赢互不影响.若中国队第n局的得分记为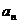 ,令
,令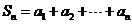 .
.
(1)求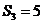 的概率;
的概率;
(2)若规定:当其中一方的积分达到或超过4分时,比赛结束,否则,继续进行.设随机变量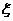 表示此次比赛共进行的局数,求
表示此次比赛共进行的局数,求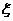 的分布列及数学期望.
的分布列及数学期望.
2.(坐标系与参数方程)求直线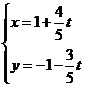 (
(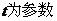 )被曲线
)被曲线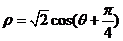 所截的弦长.
所截的弦长.
1.(矩阵与变换)设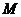 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到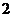 倍,纵坐标伸长到
倍,纵坐标伸长到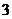 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵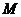 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵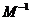 以及椭圆
以及椭圆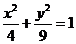 在
在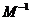 的作用下的新曲线的方程.
的作用下的新曲线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com