
题目列表(包括答案和解析)
7.已知F1、F2是双曲线16x2 -9y2 =144的焦点,P为双曲线上一点,若 |PF1||PF2| =32,
则∠F1PF2 =
A. 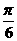 B.
B.
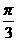
C. 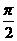 D.
D.
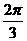
6.长轴在x轴上,短半轴长为1,两准线之间的距离最近的椭圆的标准方程是
A. 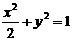 B.
B.
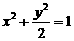
C. 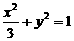 D.
D.
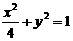
5. 已知圆C:x2 + y2-2 x-4y-20 = 0,则过原点的直线中,被圆C所截得的最长弦与最短弦的长度之和为
A. 10+4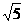 B. 10+2
B. 10+2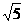
C. 5+4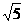 D. 5+2
D. 5+2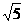
4. 下列命题中不正确的是
A. 若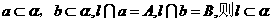
B. 若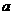 ∥
∥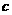 ,
,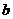 ∥
∥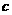 ,则
,则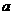 ∥
∥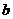
C. 若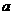
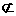
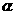 ,
,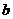
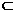
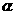 ,
,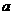 ∥
∥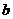 ,则
,则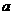 ∥
∥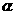
D. 若一直线上有两点在已知平面外,则直线上所有点在平面外
3.圆x2 + y2-2 x = 0和 x2 + y2 +4y = 0的位置关系是
A. 相离 B. 外切
C. 内切 D. 相交
2.双曲线3x2 -y2 =3的渐近线方程是
A. y = ±3x
B. y = ±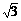 x
x
C. y =±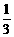 x
D. y = ±
x
D. y = ±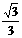 x
x
1. 若直线x = 1的倾斜角为α ,则α
A. 等于0
B. 等于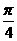
C. 等于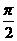 D.
不存在
D.
不存在
22.已知抛物线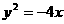 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与x轴交于点E(
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与x轴交于点E(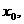 0)。
(1)求k的取值范围,
(2)求证:
0)。
(1)求k的取值范围,
(2)求证: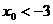 ,
(3)△PEF能否成为以EF为底的等腰三角形?若能,求出k的值,若不能,说明理由.
,
(3)△PEF能否成为以EF为底的等腰三角形?若能,求出k的值,若不能,说明理由.
21.某工厂库存A、B、C三种原料,可用来生产甲、乙两种产品,市场调查显示可获利润等各数据如下表:
|
|
A |
B |
C |
每件产品利润(元) |
|
|
库存量(件) |
100 |
125 |
156 |
(I) |
(II) |
|
甲(每件用料) |
1 |
2 |
3 |
2000 |
1000 |
|
乙(每件用料) |
4 |
3 |
1 |
1000 |
3000 |
问:若市场情况如(I),怎样安排生产能获得最大利润?
若市场情况如(II),怎样安排生产才能获得最大利润?
20.已知抛物线的顶点在原点,它的准线经过曲线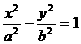 的右焦点,且与x轴垂直,抛物线与此双曲线交于点(
的右焦点,且与x轴垂直,抛物线与此双曲线交于点(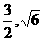 ),求抛物线与双曲线的方程.
),求抛物线与双曲线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com