
题目列表(包括答案和解析)
1.① 当平面到球心的距离小于球半径时,球面与平面的交线总是一个圆;
② 过球面上两点只能作一个球大圆; ③ 过空间四点总能作一个球;
④ 球的任意两个大圆的交点的连线是球的直径.以上四个命题中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
19.(14分)如图,在四棱锥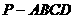 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱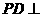 底面ABCD,
底面ABCD,
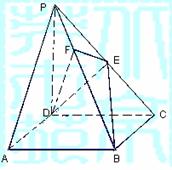
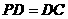 ,E是PC的中点,作
,E是PC的中点,作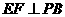 交PB于点F.
交PB于点F.
(1)证明 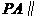 平面
平面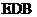 ;
;
(2)证明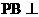 平面EFD;
平面EFD;
(3)求二面角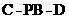 的大小.
的大小.
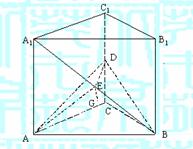 20.(14分)如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
20.(14分)如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G.
(1)求A1B与平面ABD所成角的大小
(结果用反三角函数值表示);
18.(12分)在正方体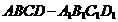 中,如图E、F分别是
中,如图E、F分别是
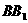 ,CD的中点,
,CD的中点,
(1)求证: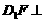 平面ADE;
平面ADE;
(2)求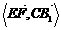 .
.
17.(12分)如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、
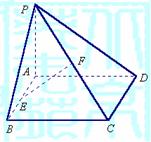 PC的中点.
PC的中点.
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与平面ABCD所成的角的大小.
15.(12分) 如图,一空间四边形ABCD的对边
AB与CD,AD与BC都互相垂直,
用向量证明:AC与BD也互相垂直.
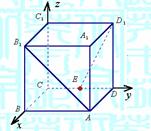 16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,
16.(12分))如图,在棱长为2的正方体ABCD-A1B1C1D1中,
E是DC的中点,取如图所示的空间直角坐标系.
(1)写出A、B1、E、D1的坐标;
(2)求AB1与D1E所成的角的余弦值.
14.设|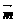 |=1,|
|=1,|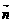 |=2,2
|=2,2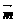 +
+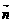 与
与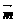 -3
-3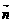 垂直,
垂直,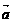 =4
=4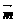 -
-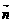 ,
,
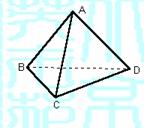
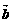 =7
=7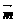 +2
+2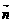 , 则<
, 则<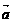 ,
,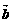 >=
.
>=
.
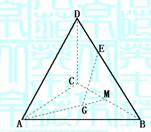
13.在空间四边形ABCD中,AC和BD为对角线,
G为△ABC的重心,E是BD上一点,BE=3ED,
以{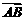 ,
,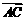 ,
,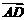 }为基底,则
}为基底,则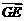 =
.
=
.
 11.若A(m+1,n-1,3),B(2m,n,m-2n),C(m+3,n-3,9)三点共线,则m+n=
.
11.若A(m+1,n-1,3),B(2m,n,m-2n),C(m+3,n-3,9)三点共线,则m+n=
.
12.已知S是△ABC所在平面外一点,D是SC的中点,
若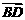 =
=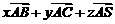 ,则x+y+z=
.
,则x+y+z=
.
10.已知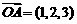 ,
,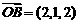 ,
,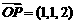 ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当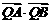
取得最小值时,点Q的坐标为 ( )
A.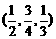 B.
B.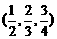 C.
C.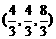 D.
D.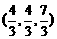
第Ⅱ卷(非选择题,共100分)
9.已知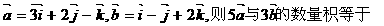 ( )
( )
A.-15 B.-5 C.-3 D.-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com