7.函数f(x)=x+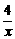+3在(－∞，－2]上(　　 )

A.无最大值，有最小值7　　　　　　　 B.无最大值，有最小值－1

C.有最大值7，有最小值－1　　　　　 D.有最大值－1，无最小值

6.两次购买同一种物品,可以有两种不同的策略.第一种是不考虑物品价格的升降,每次购买这种物品的数量一定；第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定.若两次购买这种物品时价格不相同,则两种策略中比较经济的情况为(　　 )

A.第一种策略经济　　　　　　　 B.第二种策略经济 C.两种策略同样经济　 D.不能判断

5.下列命题中，真命题有(　　 )

①若a+b＞0且ab＞0,则a＞0且b＞0　 ②若a＞b且ab＞0,则a＞b＞0　

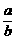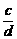
③若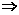＞ad＞bc　 　　　　　　　④a＞b是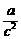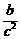＞成立的必要条件

A.①③　 　　 B.②③　　 C.②④　　　　　　　　　　 D.①④

4.角x,y满足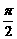－＜x＜y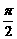＜,则x－y的取值范围是(　　 )

A.(－π,0)　 　　　 B.(－π,π)　　 　C.(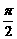－,0)　　　　　　　　　　 D.(－,)

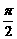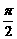3.若a＞b＞1,P=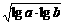,Q=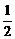(lga+lgb),R=lg(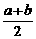),则(　　 )

A.R＜P＜Q　　　　　　　　　 B.P＜Q＜R　　　　　　　　　 C.Q＜P＜R　　　　　　　　　 D.P＜R＜Q

2.若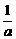<<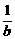0,则下列不等式:①a+b<ab；②|a|>|b|；③a<b；④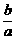+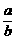>2.正确的不等式有(　　 )

A.1个　　　　　　　　　　　　　 B.2个　　　　　　　　　　　　　 C.3个　　　　　　　　　　　　　 D.4个

1.若a、b、c为实数，则下列命题正确的是(　　 )

A.若a＞b，则ac²＞bc² B.若a＜b＜0，则a²＞ab＞b²

C.若a＜b＜0，则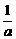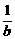＜　　 D.若a＜b＜0，则＞

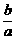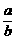
15解:∵x²+x+1＞0恒成立，

∴不等式等价于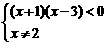

－1＜x＜2或2＜x＜3.

∴不等式的解集为{x|－1＜x＜2或2＜x＜3}.

16解:由f(x)＞1，得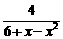＞1,

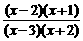化简整理得＜0.

解得－2＜x＜－1或2＜x＜3.

即f(x)＞1的解集为A={x|－2＜x＜－1或2＜x＜3}.

由g(x)＜0得x²－3ax+2a²＜0,

即(x－a)(x－2a)＜0(a＜0).

则g(x)＜0的解集为B={x|2a＜x＜a,a＜0}.

根据题意，有A∩B=.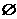

因此，a≤－2或－1≤2a＜0.

故a的范围是{a|a≤－2或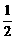－≤a＜0}.

17解:由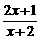<0,解得－2<x<－.

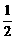∴－2<p<－.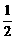

方程u²－2u+5－p²=0的判别式Δ=4(p²－4).

∵－2<p<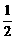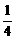－,∴<p²<4.∴Δ<0.

由此得出方程u²－2u+5－p²=0无实根.

18解:(1)由图象知，y₁=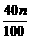+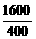=4+n,

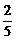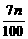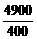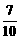y₂=+=n+.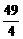

由于5＜y₁＜7,13＜y₂＜15,

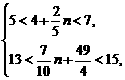∴即

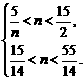
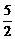∴＜n＜.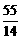

又∵n∈N,∴n=3.

(2)根据题意，得y=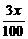+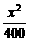≤18.4.

∴x²+12x－7360≤0,即(x+92)(x－80)≤0.

由于x＞0,∴0＜x≤80,

即行驶的最大速度为80 km/h.

19解:(1)当m²+4m－5=0,即m=1或m=－5时,显然m=1符合题意,m=－5不合题意.

(2)当m²+4m－5≠0时,要使二次不等式对一切x∈R恒成立,

必须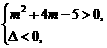

即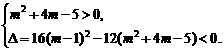

解得1<m<19.

综合(1)(2)得m的取值范围为［1,19).

20 解:由x²－x－2>0,解得x<－1或x>2.

由2x²+(5+2k)x+5k<0化为(2x+5)(x+k)<0.

∵－2是其解,∴k<2.

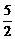∴－<x<－k.

∴原不等式组可以化为①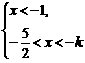或②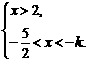

∵k<2,∴－k>－2.

∴①的整数解为－2,而要使②无整数解,只有－k≤3,

即k≥－3.∴－3≤k<2.

11. 　{x|－1≤x＜2＝ 12　 5400元 13　 1＜a＜3　 14　 －2

1:A　 2:B　 3　 A　 4.　 　A　 5　 　D　　 6　 D　 7.　 　C　 8. 　C　 9　 A　 10.　 　D