
题目列表(包括答案和解析)
19.袋中有4个白球,6个红球,在抽取这些球的时候谁也无法看到球的颜色.现先由甲取出3个球,并且取出的球将不再放回原袋中,再由乙取出4个球,若规定取得白球多者获胜,试求甲获胜的概率.
18.投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过
多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率;(Ⅱ)求该人两次投掷后得2分的概率。
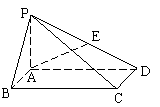
17.如图,在底面是矩形的四棱锥P-ABCD中, PA=AB=1,BC=2.(1)求证:平面PDC⊥平面PAD;(2)若E是PD的中点,求异面直线AE与PC所成角的余弦值;(3)在BC边上是否存在一点G,使得D点到平面PAG的距离为1,若存在,求出BG的值;若不存在,请说明理由。
16.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从600袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将600袋牛奶按000,001,…,599进行编号,如果从随机数表第8行第6列的数开始向右读,请你依次写出最先检测的5袋牛奶的编号 ______ ________ . (下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 59 17 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
15.有80个数,其中一半是奇数,一半是偶数,从中任取两数,则所取的两数和为偶数的概率是 .
14.对于正整数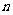 和
和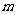 ,定义
,定义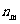 !=
!=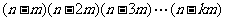 ,其中
,其中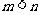 ,且
,且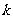 是满足
是满足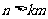 的最大整数,则(
的最大整数,则(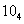 !)/(10
!)/(10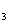 !)=___________.
!)=___________.
13.若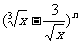 的展开式的各项系数之和为-32,那么展开式中的常数项为_________.
的展开式的各项系数之和为-32,那么展开式中的常数项为_________.
12.棱锥P一ABCDEF的底面是正六边形,侧棱PA⊥面ABF,则下列命题:
①∠PDA是侧面PDC与底面所成的二面角的平面角; ②PC的长就是点P到直线CD的距离;
③∠PCB是侧棱PC与底面所成的角;④EF的长是点E到平面AFP的距离.其中正确的命题有____________.
11. 一个正方体的六个面上分别标有字母A、B、C、D、E、F,右图是此正方体的两种不同放置,则与D面相对的面上的字母是 .
一个正方体的六个面上分别标有字母A、B、C、D、E、F,右图是此正方体的两种不同放置,则与D面相对的面上的字母是 .
10. 已知 ,方程
,方程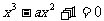 在区间(0,3)内的根的个数为
( )
在区间(0,3)内的根的个数为
( )
A.0 B.1 C.2 D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com