
题目列表(包括答案和解析)
2.证明四点共面的主要方法是四点连成两条直线,证明它们平行或相交.
4.在空间四边形 各边
各边 、
、 、
、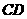 、
、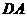 上分别取
上分别取 、
、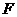 、
、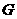 、
、 四点,如果
四点,如果 ,则有
( )
,则有
( )
A.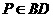 B.
B.
C.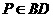 或
或 D.
D. 或
或
 [讲练平台]
[讲练平台]
例1 如图9-1,在正方体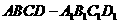 中,
中,
 为
为 的中点,
的中点,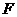 为
为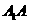 的中点.
的中点.
求证:(1)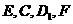 四点共面;
四点共面;
(2) 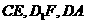 三线共点.
三线共点.
分析 要证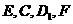 四点共面,可由这四点连成两条直线,证明它们平行或相交即可;对于(2)中证三线共点,可证两条直线的交点在第三条直线上.
四点共面,可由这四点连成两条直线,证明它们平行或相交即可;对于(2)中证三线共点,可证两条直线的交点在第三条直线上.
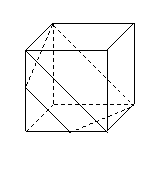 证明 (1) 如图9-2,分别连结
证明 (1) 如图9-2,分别连结
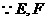 分别是
分别是 和
和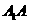 的中点,
的中点,
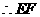
 .
.
又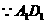
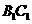
 ,
,
 是平行四边形.
是平行四边形.

 , 从而
, 从而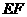 ∥
∥ .
.
根据推论3,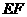 和
和 确定一个平面,故
确定一个平面,故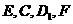 四点共面.
四点共面.
(2)
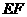
 ,
, 
 ,
,
∴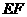
 .∴直线
.∴直线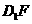 和
和 必相交.
必相交.
令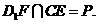 .
. 平面
平面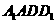 ,
,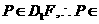 平面
平面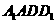 .
.
同理 平面
平面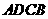 .
.
即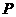 是平面
是平面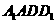 和平面
和平面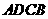 的公共点,
的公共点,
而平面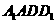
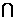 平面
平面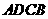 =
=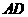 ,
,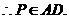
故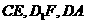 三线共点.
三线共点.
点评 1.本题也可先证明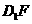 与
与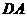 相交,
相交, 与
与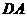 相交,且交点重合,从而证得(2),既然
相交,且交点重合,从而证得(2),既然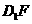 与
与 相交,那么(1)自然就成立了.
相交,那么(1)自然就成立了.
3. 一条直线和直线外四个不同的点,它们最多能确定平面的个数是 ( )
A.6 B.7 C.8 D.9
2. 下列四种说法:
(1) 两个平面可以仅有一个公共点;
(2) 空间任意四边形一定是平面图形;
(3) 三条互相平行的直线最多可确定三个平面;
(4) 有三个不同公共点的两个平面一定重合.
其中正确的个数是 ( )
A.0 B.1 C.2 D.3
1. 如果 那么下列关系成立的是
( )
那么下列关系成立的是
( )
A.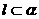 B.
B.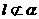 C.
C.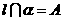 D.
D.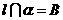
2.要掌握解题的通法,推理严谨,书写规范
(1)转化法是空间直线和平面的位置关系的判断与证明的常用方法,线线关系(主要指平行和垂直)、线面关系、面面关系三者中,每两者都存在着依存关系,充分、合理地运用这些关系是解题的关键;另外,转化法还常常运用在求距离时点的位置的变化,以及线面距、面面距间的转化;
(2)求角或距离的步骤是“一作、二证、三计算”,即先作出所求角或表示距离的线段,再证明它就是所要求的角或距离,然后再进行计算,尤其不能忽视第二步的证明.
[考点指津]
掌握平面基本性质的三条公理及公理3的三条推论,能运用它们证明空间的共点、共线、共面问题.
[知识在线]
1.必须明确本章内容的复习目标:
(1)准确理解和系统掌握空间直线和平面的各种位置关系(特别是平行与垂直的位置关系),能够运用概念、公理、定理等进行严密的推理判断和逻辑论证;
(2)正确理解空间的各种角和距离的概念,能将其转化为平面角和线段的长度,并能熟练地运用平面几何及三角知识来计算;
(3)通过图形能迅速判断几何元素的位置关系,能熟练绘制符合要求的空间图形的直观图、截面图,熟练地处理折叠、截面的问题. 但要注意立体几何中的示意图不反映元素关系的真实结构,逻辑论证仍是关键;
(4)理解用反证法证明命题的思路,会证一些简单的问题.
15.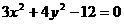 [x<0且去除点(-2,0)]
[x<0且去除点(-2,0)]
14.(1)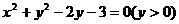 ,或
,或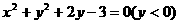
(2)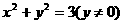
13.k=0,(1,1),(-1,1)。提示:设两交点为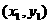 ,
,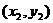 ,则
,则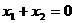
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com