
题目列表(包括答案和解析)
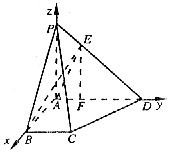
4.在棱长为1的正四面体ABCD中,E, F分别是 BC, AD的中点,则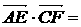 ( )
( )
A. 0
B. 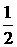 C.
C. 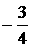 D.
D. 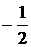
3.若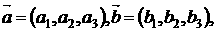 则
则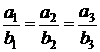 是
是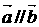 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
2.已知空间三点O(0,0, 0), A(-1, 1, 0), B(0, 1, 1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.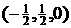 D.
D.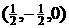
1.平行六面体 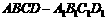 中,E,F,G,H,P,Q是
中,E,F,G,H,P,Q是 的中点,则A ( )
的中点,则A ( )
A.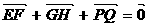 B.
B.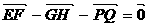
C.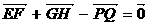 D.
D.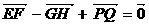
22.(本小题满分14分)
解:由已知,得A(0, 0, 0), B(a, 0, 0), C(a, a, 0), D(0, 2a, 0).……………………2分
∵PA⊥面ABCD,PD与面ABCD成30°,∴∠PDA=30°。∴P(0, 0, 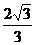 a)。…………3分
a)。…………3分
过E作EF⊥AD,垂足为F,则AE=a,∠EAF=60°,AF=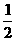 a,EF=
a,EF=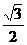 a。
a。
 ∴E(0,
∴E(0, 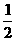 a,
a, 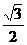 a) ………………………………4分
a) ………………………………4分
 (I)BE=(﹣a,
(I)BE=(﹣a,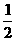 a,
a, 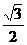 a),
a),
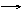 PD=(0, 2a,,﹣
PD=(0, 2a,,﹣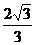 a)
a)
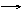
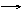 ∴BE·PD=
∴BE·PD=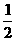 a·2a+
a·2a+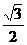 a·(﹣
a·(﹣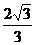 a) =0
∴BE⊥PD。…………6分
a) =0
∴BE⊥PD。…………6分

 (II)AE=(0,
(II)AE=(0,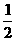 a,
a, 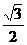 a),CD=(﹣a,a,0),
a),CD=(﹣a,a,0),
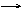
 ∴cos<AE, CD> =
∴cos<AE, CD> =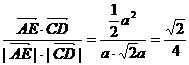 。
。
∴异面直线AE与CD所成的角为arccos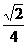 。…………………………10分
。…………………………10分

 (III)∵n⊥平面PCD,∴n⊥PD,n⊥CD,
(III)∵n⊥平面PCD,∴n⊥PD,n⊥CD,
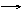
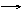 又n=(1,p,q), PD=(2, 2a, ﹣
又n=(1,p,q), PD=(2, 2a, ﹣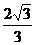 a), CD=(﹣a, a, 0),
a), CD=(﹣a, a, 0),
 ∴n·PD=0·1+2a·p-
∴n·PD=0·1+2a·p-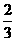
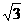 a·q=0,
a·q=0,
 n·CD=1·(﹣a)+a·p+q·0=0,…………………………12分
n·CD=1·(﹣a)+a·p+q·0=0,…………………………12分
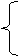
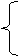 即 p-
即 p-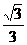 q=0 ∴ p=1
q=0 ∴ p=1
p-1=0
q=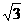 ,
,
即n的坐标为(1, 1, 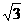 )。…………………………14分
)。…………………………14分
21.(满分14分)
解:(Ⅰ)由正方形ACC1A1与等腰直角△ACB互相
垂直,∠ACB=90°,∴BC⊥AC,∴BC⊥CC1.以C
为坐标原点,建立空间直角坐标系C-xyz,如图.(2分)
设AC=CB=a,AG=x,则A(0,a,0).
C1(0,0,a),G(0,a,x),E(-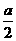 ,
,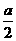 ,0).
,0).
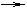 AC1=(0,-a,a),EG=(-
AC1=(0,-a,a),EG=(-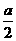 ,
,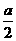 ,x).(4分)
,x).(4分)
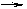
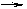 ∵AC1·EG=0,∴-
∵AC1·EG=0,∴-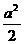 +xa=0. ∴x=
+xa=0. ∴x=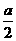 ,∴G为AA1的中点.(7分)
,∴G为AA1的中点.(7分)
(Ⅱ)∵G(0,a,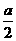 ),F(
),F(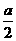 ,0,0),
,0,0),
 ∴GF=(
∴GF=(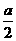 ,-a,-
,-a,-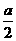 ),AC1=(0,-a,a).(9分)
),AC1=(0,-a,a).(9分)
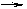 ∴ | GF | =
∴ | GF | =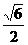 a,| AC1 | =
a,| AC1 | =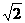 a,∴GF·AC1=a2-
a,∴GF·AC1=a2-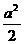 =
=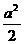 .
.
 ∴cos<AC1,GF>=
∴cos<AC1,GF>=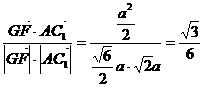 .(14分)
.(14分)
20.解法一:如图建立空间直角坐标系,
 由题意,有
由题意,有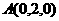 ,
,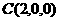 ,
,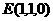
设D点的坐标为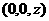
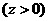 ,
,
则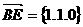 ,
,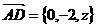
则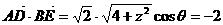 ,
,
且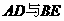 所成的角的大小为
所成的角的大小为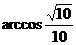 .
.
∴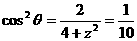 , 得
, 得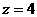 ,故BD的长度是4,
,故BD的长度是4,
又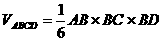 , 因此四面体ABCD的体积是
, 因此四面体ABCD的体积是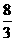 ,
,
解法二:过A引BE的平行线,交CB的延长线于F,∠DAF是异面直线BE与AD所成的角.
 ∴∠DAF=
∴∠DAF=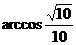 ,
,
∵E是AC的中点,∴B是CF的中点, AF=2BE=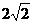 .
.
又BF,BA分别是DF,DA的射影,且BF=BC=BA, ∴DF=DA
三角形ADF是等腰三角形,
AD=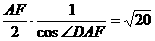 , 故
, 故 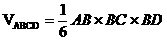 ,
,
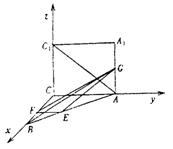 因此四面体ABCD的体积是
因此四面体ABCD的体积是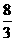 .
.
19.解:如图 建立空间直角坐标系,则B(0,0,0), A(1,0,0), M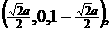
N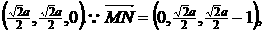

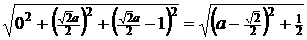 (0<a<
(0<a<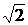 ),
),
∴当a=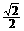 ,即M,N分别是AC,BF的中点时,MN最小,此时,M
,即M,N分别是AC,BF的中点时,MN最小,此时,M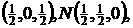
 MN的中点G
MN的中点G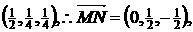
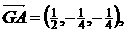
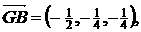 则
则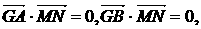
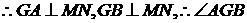 是二面角
是二面角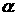 的平面角。
的平面角。
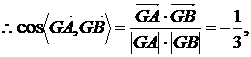 故所求二面角
故所求二面角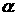 =arccos
=arccos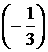 .
.
18.解:由已知,有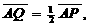 且
且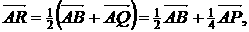
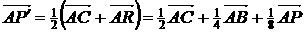 .要使P′,P重合,应有
.要使P′,P重合,应有

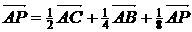 ,
,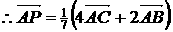 .
.
∴符合条件的不动点存在。
17.解: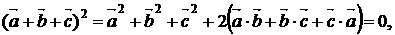
得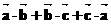 =
=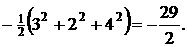
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com