
题目列表(包括答案和解析)
3.圆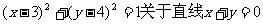 对称的圆的方程是( )
对称的圆的方程是( )
A.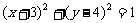 B.
B.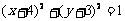
C.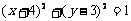 D.
D.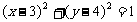
2.过点M(-4,3)和N(-2,1)的直线方程是 ( )
A.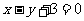 B.
B.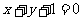 C.
C.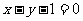 D.
D.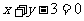
1. 如果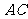 <
<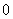 且
且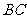 <
<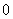 ,则直线
,则直线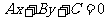 不通过
(
)
不通过
(
)
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
22. ⊿ABC是边长为2的正三角形,在⊿ABC所在平面外有一点P,PB=PC=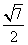 ,PA=
,PA=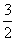 ,延长BP至D,使BD=
,延长BP至D,使BD=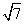 ,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
,E是BC的中点,求AE和CD所成角的大小和这两条直线间的距离.
解析:分别连接PE和CD,可证PE//CD,(2分)则∠PEA即是AE和CD所成角.(4分)在Rt⊿PBE中,
PB=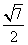 ,BE=1,∴PE=
,BE=1,∴PE=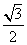 。在⊿AEP中,AE=
。在⊿AEP中,AE=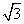 ,
,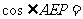
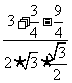 =
=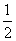 .
.
∴∠AEP=60º,即AE和CD所成角是60º.(7分)
 ∵AE⊥BC,PE⊥BC,PE//DC,∴CD⊥BC,∴CE为异面直线AE和CD的公垂线段,(12分)它们之间的距离为1.(14分)
∵AE⊥BC,PE⊥BC,PE//DC,∴CD⊥BC,∴CE为异面直线AE和CD的公垂线段,(12分)它们之间的距离为1.(14分)
21.(本小题满分12分)
某检验员在检查每件产品质量时,将合格品正确地鉴定为合格品概率以及将次品正确地鉴定为次品的概率都是90%,如果需要他鉴定3件产品,其中有2件合格品和1件次品,试求:
(I)3件产品都被鉴定为合格品的概率P1 ;
(II)3件产品都被鉴定为次品的概率P2 ;
(III)3件产品鉴定为2件合格品1件次品的概率P3 .
解:(I)用A表示将合格品鉴定为合格品,B表示将次品鉴定为次品,而用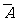 表示将合格品鉴定为次品,
表示将合格品鉴定为次品,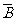 表示将次品鉴定为合格品.故
表示将次品鉴定为合格品.故
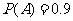 ,
,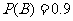 ,
,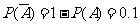 ,
,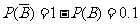
3件产品都被鉴定为合格品,说明2件合格品都被正确鉴定,而1件次品被错误地鉴定为合格品了.所以
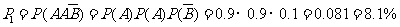 ……4分
……4分
(II)3件产品都被鉴定为次品,说明其中的1件次品被正确鉴定为次品,而2件合格品均被错误地鉴定为次品了,所以
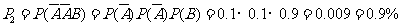 . ……8分
. ……8分
(III)3件产品鉴定为2件合格品1件次品含2种情况:
其一是把2件合格品鉴定为合格品,1件次品鉴定为次品,
其二是把其中的1件合格品鉴定为合格品,另一合格品被鉴定为次品,
并且其中的1件次品被鉴定为合格品. ……10分
故,所求概率为
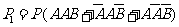
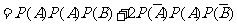

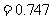
 ……12分
……12分
点评:自编题,本题考查实际生活中产品的质量检验时涉及的概率问题,在解题过程中,要求正确使用符号表示事件,用符号求事件的概率.特别是第3题,属于易错题.本题属中等题.
20.设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心。
如图:(1)证明:PQ∥平面AA1B1B;
(2)求线段PQ的长。(12分)
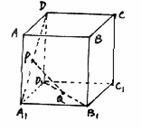

评注:本题提供了两种解法,方法一,通过平行四边形的对边平行得到“线线平行”,从而证得“线面平行”;方法二,通过三角形的中位线与底边平行得到“线线平行”,从而证得“线面平行”。本题证法较多。
19. 三个平面两两相交得三条直线,求证:这三条直线相交于同一点或两两平行.
已知:平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c.
求证:a、b、c相交于同一点,或a∥b∥c.
证明:∵α∩β=a,β∩γ=b
∴a、b β
β
∴a、b相交或a∥b.
(1)a、b相交时,不妨设a∩b=P,即P∈a,P∈b
而a、b β,a
β,a α
α
∴P∈β,P∈α,故P为α和β的公共点
又∵α∩γ=c
由公理2知P∈c
∴a、b、c都经过点P,即a、b、c三线共点.
(2)当a∥b时
∵α∩γ=c且a α,a
α,a γ
γ
∴a∥c且a∥b
∴a∥b∥c
故a、b、c两两平行.
由此可知a、b、c相交于一点或两两平行.
说明:此结论常常作为定理使用,在判断问题中经常被使用.
18.(12分)设f(x)=(1+x)m+(1+x)n(m、n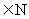 ),若其展开式中,关于x的一次项系数为11,试问:m、n取何值时,f(x)的展开式中含x2项的系数取最小值,并求出这个最小值.
),若其展开式中,关于x的一次项系数为11,试问:m、n取何值时,f(x)的展开式中含x2项的系数取最小值,并求出这个最小值.
解:展开式中,关于x的一次项系数为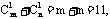 (3分)关于x的二次项系数为
(3分)关于x的二次项系数为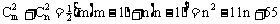 ,(8分)当n=5或6时,含x2项的系数取最小值25,此时m=6,n=5或
m=5,n=6. (12分)
,(8分)当n=5或6时,含x2项的系数取最小值25,此时m=6,n=5或
m=5,n=6. (12分)
18.如图,在棱长为2的正方体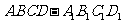 中,O是底面ABCD的中心,E是
中,O是底面ABCD的中心,E是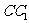 的中点.那么异面直线OE和
的中点.那么异面直线OE和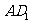 之间的距离等于
之间的距离等于 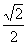
17. A是两异面直线a,b外一点,过A最多可作 一个 个平面同时与a,b平行。
A是两异面直线a,b外一点,过A最多可作 一个 个平面同时与a,b平行。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com