
题目列表(包括答案和解析)
1.a>b,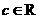 ,则( ).
,则( ).
(A)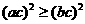 (B)
(B)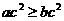 (C)
(C)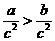 (D)
(D)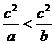
18.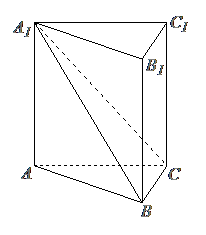 直三棱柱
直三棱柱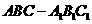 的侧棱
的侧棱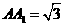 ,底面
,底面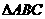 中,
中,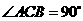 ,
,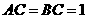 。
。
(1)求点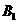 到平面
到平面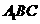 的距离;
的距离;
(2)求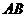 与平面
与平面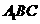 所成角的大小;
所成角的大小;
答案:(1)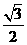 ;
;
(2)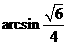 。
。
17.如图,在三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D是PA的中点,二面角P-AC-B为120°,PC=2,AB=2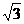 . 取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
. 取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
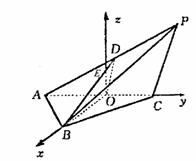 (I)求B、D、P三点的坐标;
(I)求B、D、P三点的坐标;
(II)求BD与底面ABC所成角的余弦值.
解:(I)∵O是AC中点,D是AP的中点,
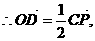
∵∠PCA=90° ∴AC⊥OD.
又∵△ABC为正三角形, ∴BO⊥AC.
∴∠BOD为二面角P-AC-B的平面角,
∴∠BOD=120°,
∵OB=Absin60°=3,∴点B的坐标为(3,0,0)…………………………2分
延长BO至F使OF⊥BF,则OF=ODcos60°=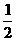 ,DF=ODsin60°=
,DF=ODsin60°=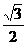 ,
,
∴点D的坐标为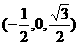 .……………………………………………………4分
.……………………………………………………4分
设点P的坐标为(x,y,z),
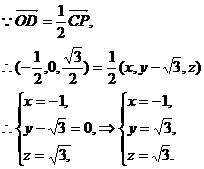
∴点P的坐标为(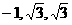 )………………………………………………6分
)………………………………………………6分
(II)∵ BD在平面ABC上的射影为BO,
∴∠OBD为BD与底面ABC所成的角.………………………………………8分

∴ BD与底面ABC所成角的余弦值为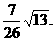 ……………………………10分
……………………………10分
16.如图,正三棱柱AC1中,AB=2,D是AB的中点,E是A1C1的中点,F是B1B中点,异面直线CF与DE所成的角为90°.
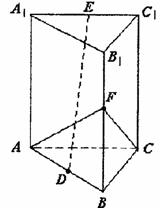 (1)求此三棱柱的高;
(1)求此三棱柱的高;
(2)求二面角C-AF-B的大小.
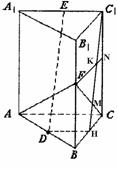 解:(1)取BC、C1C的中点分别为H、N,连结HC1,
解:(1)取BC、C1C的中点分别为H、N,连结HC1,
连结FN,交HC1于点K,则点K为HC1的中点,因
FN//HC,则△HMC∽△FMK,因H为BC中点
BC=AB=2,则KN=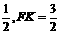 ,∴
,∴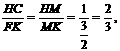
则HM=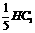 ,在Rt△HCC1,HC2=HM·HC1,
,在Rt△HCC1,HC2=HM·HC1,
解得HC1=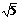 ,C1C=2.
,C1C=2.
另解:取AC中点O,以OB为x轴,OC为y轴,按右手系建立空间坐标系,设棱柱高为h,则C(0,1,0),F( ),D(
),D(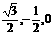 ),E(0,0,h),
),E(0,0,h),
∴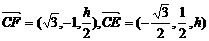 ,由CF⊥DE,得
,由CF⊥DE,得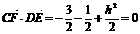 ,解得h=2.
,解得h=2.
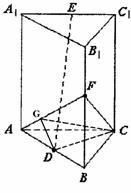
(2)连CD,易得CD⊥面AA1B1B,作DG⊥AF,连CG,
由三垂线定理得CG⊥AF,所以∠CGD是二面角C-AF-B
的平面角,又在Rt△AFB中,AD=1,BF=1,AF=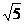 ,
,
从而DG=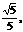 ∴tan∠CGD=
∴tan∠CGD=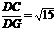 ,
,
故二面角C-AF-B大小为arctan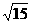 .
.
15.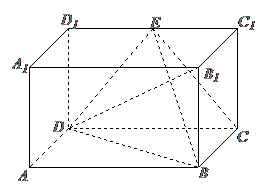 直四棱柱
直四棱柱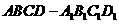 的侧棱
的侧棱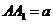 ,底面
,底面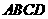 是边长
是边长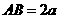 ,
,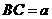 的矩形,
的矩形,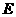 为
为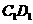 的中点.
的中点.
(Ⅰ)求证:平面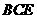 ⊥平面
⊥平面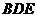 ;
;
(Ⅱ)求二面角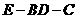 的大小。
的大小。
(Ⅰ)证明:∵E是C1D1的中点,∴C1E=D1E=a,又由直四棱柱的性质得BC⊥面CC1D1D,
∴EC=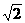 a,BE=
a,BE=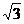 a,DE=
a,DE=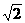 a,又BD=
a,又BD=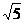 a,
a,
∴△BDE是直角三角形,△DEC也是直角三角形,∴DE⊥EC,DE⊥BE,∴DE⊥面BEC,又DE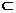 平面BDE ∴平面BCE⊥平面BDE 4分
平面BDE ∴平面BCE⊥平面BDE 4分
(Ⅱ)解:取CD的中点E′ ∴EE′⊥面ABCD,∴△BED在面AC内的射影是
△E′BD,设二面角E-BD-C的大小为θ,∴cosθ=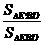
又∵S△BDE=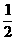 DE·BE=
DE·BE=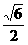 a2,S△BE′D=
a2,S△BE′D=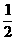 a2,
a2,
∴cosθ=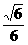 ∴θ=arccos
∴θ=arccos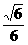 8分
8分
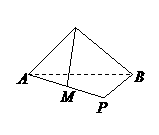
14.在△ABC中,∠ABC=90°,AB=BC=a,BD⊥AC于D,以BD为棱折成直二面角
A-BD-C,P是AB上的一点,若二面角P-CD-B为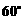 ,则AP= .
,则AP= .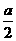
13.长方体的对角线长为8,长、宽、高的和为14,则它的全面积为 132 .
12.在30°二面角的一个面内有一条直线与二面角的棱成30°角,则此直线与二面角的
另一个面所成的角的正弦值为 ;
11.在 中,
中,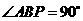 ,
,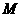 是
是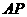 的中点,
的中点,
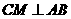 ,
, ,
,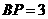 ,则异面直线
,则异面直线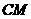
与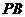 的距离为
;2
的距离为
;2
10.若点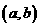 是直线
是直线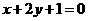 上的一个动点,则
上的一个动点,则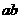 的最大值是 ( C )
的最大值是 ( C )
A. 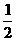 B.
B. 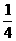 C.
C.
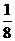 D.
D. 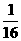
请将选择题的答案填写在下面的表格中:
 二.填空题
二.填空题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com