
题目列表(包括答案和解析)
4.将边长为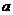 的正方形
的正方形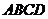 沿对角线
沿对角线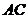 折起,使得
折起,使得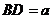 ,则三棱锥
,则三棱锥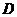 -
-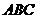 的体积为 ( )
的体积为 ( )
A.
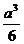 B.
B.
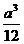 C.
C.
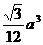 D.
D.
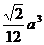
3.下列命题正确的是 ( )
A. 过平面外的一条直线只能作一平面与此平面垂直
B. 平面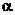 ⊥平面
⊥平面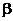 于
于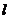 ,
,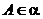 ,
,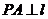 ,则
,则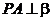
C. 一直线与平面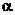 的一条斜线垂直,则必与斜线的射影垂直
的一条斜线垂直,则必与斜线的射影垂直
D. 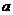 、
、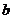 、
、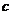 是两两互相垂直的异面直线,
是两两互相垂直的异面直线, 为
为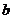 、
、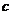 的公垂线,则
的公垂线,则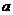 ∥
∥
2.在下列条件中,可判断平面α与β平行的是 ( )
A.α、β都垂直于平面r.
B.α内存在不共线的三点到β的距离相等.
C.l,m是α内两条直线,且l∥β,m∥β.
D.l,m是两条异面直线,且l∥α,m∥α, l∥β,m∥β.
1.已知直线l⊥平面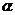 ,直线m
,直线m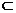 平面
平面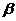 ,则下列命题中正确的是 ( )
,则下列命题中正确的是 ( )
A.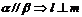 B.
B.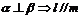 C.
C.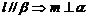 D.
D.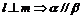
21.(本小题满分12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且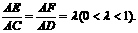
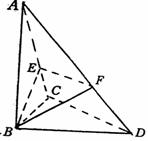 (Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
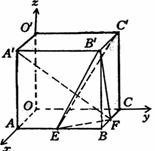 22.(本小题满分13分)棱长为a的正方体OABC-O′A′B′C′中,E、F分别为棱AB、BC上的中点, 如图所示,以O为原点,直线OA、OC、OO′分别为x、y、z轴建立空间直角坐标系.
22.(本小题满分13分)棱长为a的正方体OABC-O′A′B′C′中,E、F分别为棱AB、BC上的中点, 如图所示,以O为原点,直线OA、OC、OO′分别为x、y、z轴建立空间直角坐标系.
(Ⅰ)求证:A′F⊥C′E;
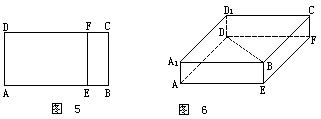
20.(本小题满分12分)
有一矩形纸片ABCD,AB=5,BC=2,E,F分别是AB,CD上的点,且BE=CF=1,把纸片沿EF折成直二面角.
(1)求BD的距离;
(2)求证AC,BD交于一点且被这点平分.
19.(本小题满分12分)已知空间四边形ABCD的边长都是1,又BD=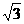 ,当三棱锥A-BCD的体积最大时,求二面角B-AC-D的余弦值。
,当三棱锥A-BCD的体积最大时,求二面角B-AC-D的余弦值。
17.(本小题满分10分)已知矩形ABCD的边AB=1,BC=a,PA⊥平面ABCD,PA=1,问
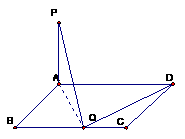 BC边上是否存在点Q,使得PQ⊥QD,并说明理由.
BC边上是否存在点Q,使得PQ⊥QD,并说明理由.
 18.(本小题满分15分)如图,正三棱柱ABC-A1B1C1的底面边长的3,侧棱AA1=
18.(本小题满分15分)如图,正三棱柱ABC-A1B1C1的底面边长的3,侧棱AA1=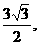 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1-AD-B的大小;
(Ⅲ)求三棱锥C1-ABB1的体积.
16.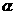 、
、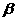 是两个不同的平面,
是两个不同的平面, 、
、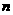 是平面
是平面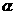 及
及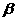 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
① ⊥
⊥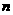 ②
②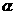 ⊥
⊥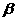 ③
③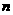 ⊥
⊥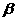 ④
④ ⊥
⊥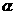
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: _________________________.
15.与正方形各面成相等的角且过正方体三个顶点的截面的个数是________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com