
题目列表(包括答案和解析)
7.Rt△ABC的斜边AB的长度等于定值C,顶点A、B在x轴,y轴上滑动,则斜边AB的中点M的轨迹方程为
6.已知A(-1,0),B(2,4),且△ABC的面积是10,则点C的轨迹方程是 .
5.已知点A(0,-1),点B是抛物线y=2x2+1上的一个动点,则线段AB的中点的轨迹是( )
A.抛物线y=2x2 B.抛物线y=4x2
C.抛物线y=6x2 D.抛物线y=8x2
4.方程4x2-y2+4x+2y=0表示的曲线是( )
A.一个点 B.两条互相平行的直线
C.两条互相垂直的直线 D.两条相交但不垂直的直线
3.动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A.y=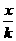 (x≠0) B.y=kx(x≠0)
(x≠0) B.y=kx(x≠0)
C.y=-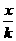 (x≠0) D.y=±kx(x≠0)
(x≠0) D.y=±kx(x≠0)
2.若点M到x轴的距离和它到直线y=8的距离相等,则点M的轨迹方程是( )
A.x=-4 B.x=4 C.y=-4 D.y=4
1.曲线f(x,y)=0关于直线x-y-2=0的对称曲线的方程为( )
A.f(y+2,x)=0 B.f(x-2,y)=0
C.f(y+2,x-2)=0 D.f(y-2,x+2)=0
2.点P是双曲线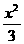 -
-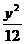 =1右分支上任意一点,F1,F2分别为左、右焦点,设∠PF1F2=α,∠PF2F1=β,求证:3tan
=1右分支上任意一点,F1,F2分别为左、右焦点,设∠PF1F2=α,∠PF2F1=β,求证:3tan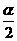 =tan
=tan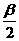 .
.
解:在△PF1F2中,利用正弦定理及分比定理得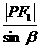 =
=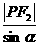 =
=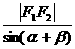 =
=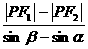 ,
,
∴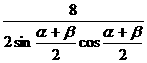 =
=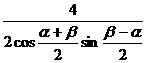 ,即2sin
,即2sin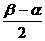 =sin
=sin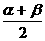 ,展开并简化,得3sin
,展开并简化,得3sin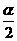 cos
cos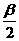 =sin
=sin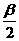 cos
cos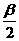 ,
,
∴3tan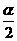 =tan
=tan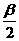 .
.
[知识探究学习]
舰A在舰B的正东6km处,舰C在舰B的北偏西30°且与B相距4千米处,它们准备围捕海洋动物.某时刻A发现动物信号,4s后B、C同时发现这种信号,A发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度是1km/s,炮弹的速度是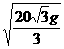 km/s,其中g为重力加速度.若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
km/s,其中g为重力加速度.若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
解:取AB所在直线为x轴,AB中点为原点建立直角坐标系,则A、B、C舰的坐标分别为(3,0)、(-3,0)、(-5,2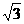 ).
).
记动物所在位置为P,则|PB|=|PC|,于是P在BC中垂线上,其方程为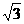 x-3y+7
x-3y+7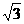 =0.
=0.
又A、C两舰发现信号的时间差为4秒,有|PB|-|PA|=4,于是P在双曲线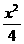 -
-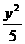 =1的右支上,求得P点坐标是(8,5
=1的右支上,求得P点坐标是(8,5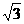 )且|PA|=10.
)且|PA|=10.
又kPA=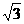 ,∴直线PA的倾斜角为60°,于是舰A发射炮弹的方位角是北偏东30°,
,∴直线PA的倾斜角为60°,于是舰A发射炮弹的方位角是北偏东30°,
设发射的仰角是θ,初速度为v0=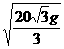 ,则
,则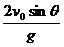 =
=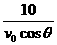 ,
,
∴sin2θ=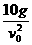 =
=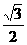 ,
,
∴仰角θ=30°
1.已知双曲线2x2-y2=2,试问过点N(1,1)能否作一直线与双曲线交于C、D两点,且使N为CD的中点?这样的直线如果存在,求出它的方程,如果不存在,则说明理由.
将问题一般化:N(x0,y0),双曲线方程为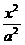 -
-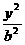 =1,若过点N的双曲线的中点弦存在,则N点应在什么位置?其方程又为何?
=1,若过点N的双曲线的中点弦存在,则N点应在什么位置?其方程又为何?
2.双曲线型自然通风塔的外形,是双曲线的一部分绕其虚构旋转所成的曲面,它的最小半径是6米,最小半径处的截口平面到地面距离是5米,底面截口半径是10米,求此双曲线的标准方程.
注:这是一个有实际意义的题目.解这类题目时,首先要确认以下两个问题:(1)选择适当的坐标系;(2)将实际问题中的条件借助坐标系用数学语言表达出来.双曲线的标准方程为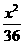 -
-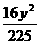 =1.
=1.
[知识验证实验]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com