2.防空探照灯的反射镜与过轴的截面的交线是一条抛物线.已知灯口直径是2000mm,深度是800mm.光源应放在什么位置?

答：光源应放在反光曲面轴上距顶点312.5mm处.

1.求证：以抛物线的焦点弦为直径的圆必与抛物线的准线相切.

若将抛物线换成椭圆、双曲线，结论又如何.

3.某隧道横断面由抛物线拱顶与矩形三边组成，尺寸如图.某卡在空车时能过此隧道，现载一集装箱，箱宽3米，车与箱共高4.5米，此车能否通过此隧道，说明理由.

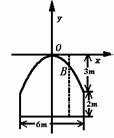
分析　 车隧道横断面(如图)进行研究，关键是看在离隧道中心线1.5米处，隧道顶高是否有4.5米，(这只是理论上的研究，实际通过时还应留有余地)适当建立直角坐标系，利用抛物线的标准方程，会使计算更方便一些.

如图建立直角坐标系.设抛物线标准方程为x²=-2py，则点(3，-3)在抛物线上，求得P=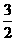,上拱抛物线方程为x²=-3y,箱宽3米，故当x=1.5米时，y=-0.75米即B(1.5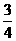，-)，那么B点到底的距离为5-0.75=4.25米

而车与箱的高为4.5米，故不能通过.

[知识验证实验]

抛物线y²=2x上的点P(x,y)到点A(a,0)(a∈R)的距离的最小值记为f(a).

(1)求f(a)的表达式；

(2)当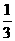≤a≤5时，求f(a)的最大值和最小值.

分析　 (1)｜PA｜===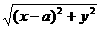

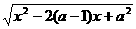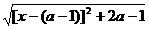
当a-1＜0,即a＜1时，f(a)=｜a｜,当a-1≥0,即a≥1时，f(a)= .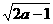

∴f(a)=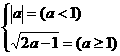 　

(2)当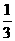≤a≤5时

f_min=f()=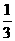

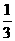
f_max=f(5)=3.

解：(1)｜PA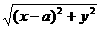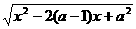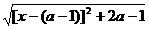｜===,当a-1＜0，即a＜1时，f(a)=｜a｜,当a-1≥0,即a≥1时，f(a)= 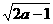,∴f(a)=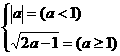 　

(2)当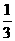≤a≤5时，①若a∈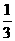［,1］,f(a)=a为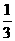［,1］上的增函数.∴f_min=f(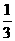)=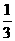,②若a∈［1,5］,f(a)= 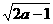为［1,5］上增函数，∴f_max=f(5)= 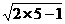　=3，综上知：f(a)的最大值为3，最小值为.

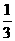[知识探究学习]

2.过抛物线y²=2px上一点P(x₀,y₀)的切线方程为　　　　　 　　.

提示：用上题结论y=kx+m=kx+y₀-kx₀.

m=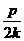=y₀-kx₀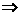k=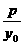

1.证明直线y=kx+m与抛物线y²=2px相切的充要条件是m=.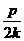

10.设抛物线C：y²=2px(p＞0)上有两动点A、B(AB不垂直于x轴)，F为焦点，且｜AF｜+｜BF｜=8，又线段AB的垂直平分线恒过定点Q(6，0).(1)求抛物线C的方程；(2)求△AQB的面积最大值.

[生活实际运用]

9.设抛物线y²=2px(p＞0)的弦PQ交x轴于点R，过P、Q分别作x轴的垂线，垂足分别为M、N，求证：｜OR｜是｜OM｜和｜ON｜的等比中项.

8.定点A(3，2)是抛物线y²=2px(p＞0)内部的一点，F是抛物线的焦点，点Q在抛物线上移动，已知｜AQ｜+｜QF｜的最小值为4，则P=　　　　　　　 .

7.抛物线y²=16x上的一点P到x轴的距离为12，则P与焦点F间的距离｜PF｜=　　　　　　　 ；

6.已知抛物线y²=4ax(a＞0)上一点A(m,n)到焦点F的距离为4a，则m=　　　　　 ,n=　　　　　　　　　　 .