
题目列表(包括答案和解析)
16.(本小题满分10分)甲、乙两人解关于x的方程:log2x+b+clogx2=0,甲写错了常数b,得到根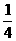 、
、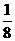 ;乙写错了常数c,得到根
;乙写错了常数c,得到根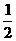 、64.求这个方程真正的根.
、64.求这个方程真正的根.
解:原方程可变形为log22x+blog2x+c=0.
由于甲写错了常数b,得到的根为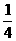 和
和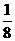 ,
,
∴c=log2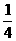 ·log2
·log2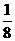 =6.
=6.
由于乙写错了常数c,得到的根为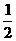 和64,
和64,
∴b=-(log2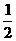 +log264)=-5.
+log264)=-5.
故原方程为log22x-5log2x+6=0.
因式分解得(log2x-2)(log2x-3)=0.
∴log2x=2或log2x=3,即x=4或x=8.
0.9t=0.5,
lg0.9t=lg0.5,
tlg0.9=lg0.5,
t=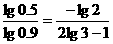 ≈6.6(年),
≈6.6(年),
即这种放射性元素的半衰期约为6.6年.
15.(本小题满分8分)
一种放射性元素,最初的质量为500 g,按每年10%衰减.
(1)求t年后,这种放射性元素质量ω的表达式;
(2)由求出的函数表达式,求这种放射性元素的半衰期(剩留量为原来的一半所需的时间叫做半衰期).(精确到0.1.已知lg2=0.3010,lg3=0.4771)
解:(1)最初的质量为500 g.
经过1年后,ω=500(1-10%)=500×0.91;
经过2年后,ω=500×0.9(1-10%)=500×0.92;
由此推知,t年后,ω=500×0.9t.
(2)解方程500×0.9t=250,
14.关于x的方程7x+1-7x·a-a-5=0有负根,则a的取值范围是_________.
解法一:由7x+1-7x·a-a-5=0得a=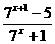 =7-
=7-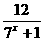 ,
,
∵x<0,∴1<7x+1<2.
∴6<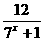 <12.
<12.
∴-5<a<1.
解法二:由7x+1-7x·a-a-5=0得7x=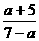 .
.
∵x<0,∴0<7x<1.∴0<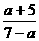 <1.
<1.
解得-5<a<1.
答案:-5<a<1
13.若不等式3x2-2ax>(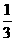 )x+1对一切实数x恒成立,则实数a的取值范围为_______.
)x+1对一切实数x恒成立,则实数a的取值范围为_______.
解析:由题意知x2-2ax>-x-1恒成立,
即x2-(2a-1)x+1>0恒成立.
故Δ=(2a-1)2-4<0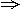 -
-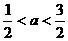 .
.
答案:-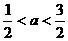
12.1992年底世界人口达到54.8亿,若人口的年平均增长率为1%,经过x年后世界人口数为 y亿,则y与x的函数解析式为_________.
解析:1992年底世界人口为54.8亿.
1年后的人口数为
y1=54.8+54.8×1%=54.8×(1+1%);
2年后的人口数为
y2=54.8×(1+1%)+54.8×(1+1%)×1%=54.8×(1+1%)2;
3年后的人口数为
y3=54.8×(1+1%)3;
……
x年后的人口数为y=54.8×(1+1%)x.
答案:y=54.8×(1+1%)x
11.方程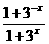 =3的解是_________.
=3的解是_________.
解析:由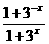 =3得3·32x+2·3x-1=0.
=3得3·32x+2·3x-1=0.
∴3x=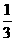 或3x=-1(舍).
或3x=-1(舍).
∴x=-1.
答案:-1
10.设lg2=a,lg3=b,则log512等于
A.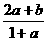 B.
B.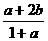
C.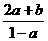 D.
D.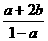
解析:log512=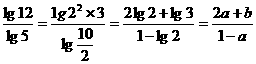 .
.
答案:C
第Ⅱ卷(非选择题 共70分)
9.右图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a、b、c、d与1的大小关系是
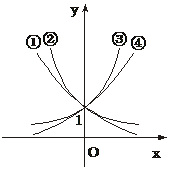
A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
解析:因为任何底数的一次幂都是底数本身,所以,可作直线x=1,它同各个图象相交,交点的纵坐标就是各指数函数的底数.
答案:B
8.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
A.(0,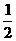 ) B.(0,
) B.(0,
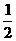 ]
]
C.( 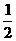 ,+∞) D.(0,+∞)
,+∞) D.(0,+∞)
解析:f(x)=log2a(x+1)>0=log2a1.
∵x∈(-1,0),∴0<x+1<1.
∴0<2a<1,即0<a<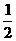 .
.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com