10.在等差数列{a_n}中，若S₉=18,S_n=240,a_n－4=30,则n的值为

A.14　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.15

C.16　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.17

解析：S₉=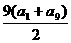=18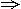a₁+a₉=4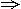2(a₁+4d)=4.

∴a₁+4d=2.又a_n=a_n－4+4d,∴S_n=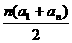=16n=240.

∴n=15.

答案：B

第Ⅱ卷(非选择题　共70分)

9.已知{a_n}是递增数列，且对任意n∈N^*都有a_n=n²+λn恒成立，则实数λ的取值范围是

A.(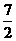－,+∞)　　　　　　　　　　　　　　　　　　　　　　　　　 B.(0,+∞)

C.(－2,+∞)　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－3,+∞)

解析：由{a_n}为递增数列得a_n+1－a_n=2n+1+λ＞0恒成立,即λ＞－2n－1在n≥1时恒成立，只需λ＞(－2n－1)_max=－3,故选D.

答案：D

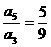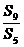8.设S_n是等差数列前n项的和，若,则等于

A.1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.－1

C.2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.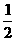

解法一：∵,∴=.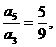

∴.

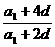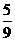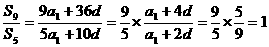解法二：∵,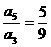

∴

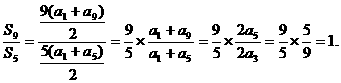
答案：A

7.已知等差数列{a_n}的公差为正数，且a₃·a₇=－12,a₄+a₆=－4,则S₂₀为

A.180　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.－180

C.90　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.－90

解析：由等差数列性质，a₄+a₆=a₃+a₇=－4与a₃·a₇=－12联立，即a₃、a₇是方程x²+4x－12=0的两根.又公差d>0,∴a₇>a₃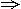a₇=2,a₃=－6,从而得a₁=－10,d=2,S₂₀=180.

答案：A

6.等差数列{a_n}中，a₄+a₇+a₁₀=57,a₄+a₅+…+a₁₄=275,a_k=61,则k等于

A.18　　　　　　　　　　　　　　　　　 B.19　　　　　　　　　　　　　　　　　 C.20　　　　　　　　　　　　　　　　　 D.21

解析：∵3a₇=a₄+a₇+a₁₀=57,∴a₇=19.由a₄+a₅+…+a₁₄=275,可得a₉=25.∴公差d=3.　　　 ∵a_k=a₉+(k－9)·d,∴61=25+(k－9)×3,解得k=21.

答案：D

5.已知等差数列{a_n}中公差d≠0.若n≥2,n∈N^*,则

A.a₁a_n+1＜a₂a_n B.a₁+a_n+1＞a₂+a_n

C.a₁+a_n+1＜a₂+a_n D.a₁a_n+1＞a₂a_n

解析：a₁a_n+1－a₂a_n=a₁(a₁+nd)－(a₁+d)［a₁+(n－1)d］=－(n－1)d²＜0,∴a₁a_n+1＜a₂a_n.

答案：A

4.设函数f(x)满足f(n+1)=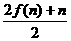(n∈N^*)且f(1)=2,则f(20)为

A.95　　　　　　　　　　　　　　　　　 B.97　　　　　　　　　　　　　　　　　 C.105　　　　　　　　　　　　　 D.192

解析：f(n+1)－f(n)=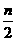

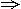
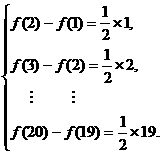
各式相加得f(20)－f(1)=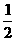(1+2+…+19) f(20)=95+f(1)=97.

答案：B

3.若数列{a_n}的前n项和S_n=n²－2n+3，则此数列的前3项依次为

A.－1,1,3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.2,1,3

C.6,1,3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.2,3,6

解析：当n=1时，a₁=S₁=1²－2×1+3=2;

当n=2时，由S₂=a₁+a₂=2²－2×2+3,得a₂=1;

当n=3时，由S₃=a₁+a₂+a₃=3²－2×3+3,得a₃=3.

答案：B

2.在数列{a_n}中，a₁=1,a_n+1=a_n²－1(n≥1),则a₁+a₂+a₃+a₄+a₅等于

A.－1　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　　 C.0　　　　　　　　　　　　　　　 D.2

解析：由已知：a_n+1=a_n²－1=(a_n+1)(a_n－1),

∴a₂=0,a₃=－1,a₄=0,a₅=－1.

答案：A

1.在100至500之间的正整数能被11整除的个数为

A.34　　　　　　　　　　　　　　　　　 B.35　　　　　　　　　　　　　　　　　 C.36　　　　　　　　　　　　　　　　　 D.37

解析：观察出100至500之间能被11整除的数为110，121，132，…，它们构成一个等差数列，公差为11，a_n=110+(n－1)·11=11n+99,由a_n≤500,解得n≤36.4,n∈N^*,∴n≤36.

答案：C