
题目列表(包括答案和解析)
17.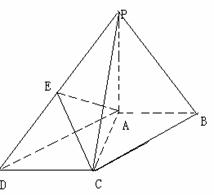 (4+4+4=12分)如图,在底面为平行四边形的四棱锥
(4+4+4=12分)如图,在底面为平行四边形的四棱锥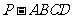 中,
中,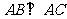 ,
,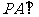 平面
平面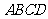 ,且
,且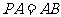 ,点
,点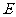 是
是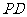 的中点.
的中点.
(Ⅰ)求证: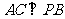 ;
;
(Ⅱ)求证: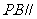 平面
平面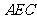
(Ⅲ)求二面角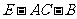 的大小.
的大小.
18题.( 6+6=12分)洞口三中本届高三即将毕业的学生罗奕同学,学习踏实,成绩拨尖,据现有的情况分析预测,她在今年六月的高考中,语、数、英三科成绩,夺取全县第一的概率:语文可达0.9,数学可达0.8,英语可达0.85,据此,请你估测:在今年的高考中:
(1)罗奕同学三科成绩均未能夺得全县第一的概率是多少?
(2)罗奕同学恰有一科成绩未夺得全县第一的概率是多少?
19题.(6+6=12分)已知()n展开式中的倒数第三项的系数为45,
求:⑴写出其展开式中含x3的项;
⑵写出其展开式中系数最大的项.
20(7+7=14分).美国NBA篮球总决赛采用七局四胜制,即先胜四局的队获胜,比赛结束。2007年美国东部活塞队与西部马刺队分别进入总决赛,已知马刺队与活塞队的实力相当,即单局比赛每队获胜的概率均为;若第一场比赛组织者可获门票收入30万美元,以后每一场门票收入都比上一场增加10万美元,设各局比赛相互之间没有影响.
①、求组织者在本次比赛中获门票收入为180万美元的概率;
②、若组织者在本次比赛中获门票收入不低于330万美元,其概率为多少.
16、(3+3+3+3=12分)中考后,洞口三中288班要从5名男生中,3 名女生中选出5人担任5门不同学科的课代表,请分别求出满足下列条件的方法数目:
①、所安排的女生人数必须少于男生 ;
②、其中的女生王丽丽指定是担任语文课代表的;
③、其中的男生付勇波必须是课代表,但又不能担任数学课代表;
④、女生王丽丽必须担任语文课代表,且男生付勇波必须担任课代表,但又不担任数学课代表。
15.已知m、n是直线,α、β、γ是平面,给出下列命题:
①若α⊥β,α∩β=m,n⊥m ,则n⊥α或n⊥β;②若α∥β,α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;④若α∩β=m,n∥m,且nËα,nËβ,
则n∥α且n∥β.其中正确的命题序号是 ________(注:把你认为正确的命题的序号都填上)
(一)、选择题答案
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
(二)、填空题答案:11题____________; 12题____________; 13题_______________;
14题____________________; 15题____________________;
14.有一块三角板ABC,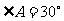 ,
,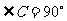 ,
,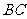 边是贴于桌面上的,当三角板与桌面成
边是贴于桌面上的,当三角板与桌面成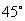 时,
时,
则AB边与桌面所成的角的正弦值是 。
13、在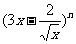 展开式中第9项为常数,则n的值为
展开式中第9项为常数,则n的值为
12、洞口三中欲安排蒋老师、杨老师等七位老师在十月一日至七日加班,每人加班一天,但蒋老师和杨老师又都不能安排在十月一日和二日,则不同的安排方法共有________种(用数字作答)
11、若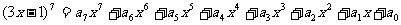 ,
,
则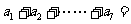
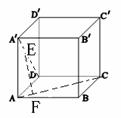
10.如图,在正方体ABCD-A′B′C′D′中,EF是异面直线AC与A′D的公垂线,
则由正方体的八个顶点所连接的直线中,与EF平行的直线:
A 有且只有一条 B 有二条 C 有四条 D 不存在
9. 在
在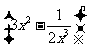 的展开式中含有常数项,则正整数n的最小值是:
的展开式中含有常数项,则正整数n的最小值是:
(A)4 (B) 5 (C) 6 (D) 7
8.用0,1,2,3,4这五个数字组成无重复数字的五位数,要求奇数数字相邻,偶数数字也相邻,
这样的数共有多少个:(A)20个 (B)24个 (C)32个 (D)36个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com