1、×√×

2-4、DDD

5、相交.　 6、平行　 7、垂直.

09052

11、(1)∵ PA⊥平面ABC，∴PA⊥BC　 ，∵ PC⊥BC，

∴ BC⊥平面APC ，∴ AH⊥BC ，PC⊥AH，∴AH⊥平面PBC ，∴平面CAH⊥平面PBC ；

(2)取BP中点G ，连GH ，∵∠PBA=45^O ，∴GA⊥BP ，

∵AH⊥平面PBC，由三垂线逆定理知，GH⊥BP，

∴∠HGA是二面角A-PB-C的平面角，

∵∠B=30⁰ ，在Rt△ABC中，设AC=a ，AB=AP=2a ，

由AH·PC=AP·AC ，易知AH= ,在Rt△AGH中,AG=PB/2= , ∴sin∠HGA= ,　　　 ∴∠HGA=arcsin ;

09051

1-4、CDDC

10、(1)由中位线知 EF∥AB∥CD ，∴EF∥平面PDC ，OF∥ PD ，∴OF∥平面PDC ，∴平面EFO∥平面PDC 。

(2)取CD中点G ，OG是OE到平面PDC的距离 ，易知OG=1 ，∴OE到平面PDC的距离为1 。

6、1㎝或5㎝　 7、 36cm或6cm　　　 8、5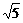　 9、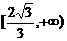

11、证明：设正四面体的棱长为a．∵AO是高,∴O是正三角形BCD的中心．

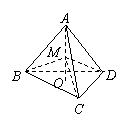连结OD,则OD=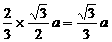．在Rt△AOD中,AO=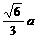,OM=；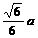

在Rt△MOD中，DM=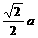．同理CM=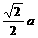，∴CM²+DM²=CD²．

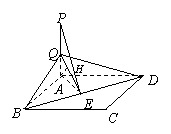∴CM^DM．同理BM^CM，DM^BM．∴BM、CM、DM两两垂直．

解：(1)在矩形ABCD中，作AE^BD于E，连结QE．

∵QA^平面ABCD，由三垂线定理得QE^BE，∴QE的

长是Q到BD的距离．在矩形ABCD中，AB=a，AD=b，

∴AE=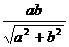．在Rt△QAE中，QA=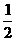PA=c，

∴QE=．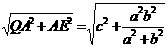

∴Q到BD的距离为．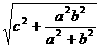

(2)∵平面BQD经过线段PA的中点，∴P到平面BQD的距离等于A到平面BQD的距离．在△AQE中，作AH^QE于E．∵BD^AE，BD^QE，∴BD^平面AQE．∴BD^AH，AH^平面BQE，即AH为A到平面BQD的距离．

在Rt△AQE中，∵AQ=c，AE=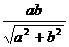，∴AH=．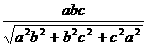

　　 ∴P到平面BQD的距离为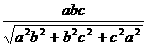

09046

1-5、DCACB　

6、内 ，外 ，垂　 7、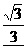 8、b∥a 或 b ⊂　 a　　 9、25或39　 10、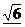

10、(2) 5cm.

09045

1-5、DBACD

11、(1) 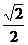a;　 (2) 45°.

7、h ;　 8、内心 ；9、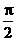;θ.　 10、60°