
题目列表(包括答案和解析)
1. 直线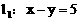 到直线
到直线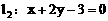 的角是( )
的角是( )
A.  B.
B. 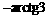 C.
C. 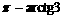 D.
D. 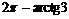
20.已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为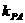 和
和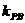 ,且满足
,且满足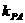 ·
·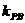 =t (t≠0且t≠-1).
=t (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
19.椭圆的两焦点分别为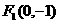 、
、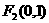 ,直线
,直线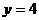 是椭圆的一条准线.
是椭圆的一条准线.
(1)求椭圆的方程;
(2)设点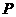 在椭圆上,且
在椭圆上,且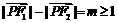 ,求
,求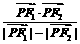 的最大值和最小值.
的最大值和最小值.
17.已知抛物线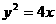 的焦点为,过
的焦点为,过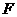 作两条互相垂直的弦
作两条互相垂直的弦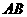 、
、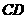 ,设
,设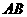 、
、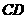 的中点分别为
的中点分别为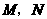 .
.
(1) 求证:直线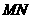 必过定点;
必过定点;
(2)分别以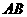 和
和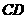 为直径作圆,求两圆相交弦中点
为直径作圆,求两圆相交弦中点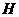 的轨迹方程.
的轨迹方程.
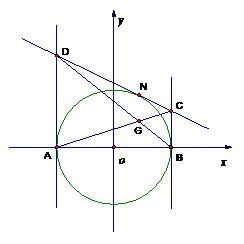 18设
18设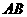 是单位圆
是单位圆 的直径,
的直径,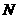 是圆上的动点,过点
是圆上的动点,过点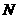 的切线与过点
的切线与过点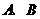 的切线分别交于
的切线分别交于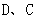 两点. 四边形
两点. 四边形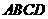 的对角线
的对角线 和
和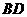 的交点为
的交点为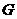 ,求
,求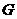 的轨迹.
的轨迹.
16.(2004年湖南高考·理工类第16题)设F是椭圆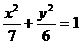 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
15.(2004年湖南高考·文史类第15题)F1,F2是椭圆C: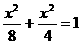 的焦点,在C上满足PF1⊥PF2的点P的个数为__________.
的焦点,在C上满足PF1⊥PF2的点P的个数为__________.
14.(2004年全国·理16)设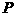 是曲线
是曲线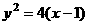 上的一个动点,则点
上的一个动点,则点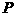 到点
到点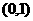 的距离与点
的距离与点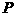 到
到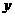 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.
13.(2004年全国文16)设P为圆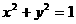 上的动点,则点P到直线
上的动点,则点P到直线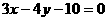 的距离的最小值为
.
的距离的最小值为
.
12.(2004年全国·理14)由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 .
11.(2004年全国文7)已知函数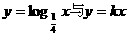 的图象有公共点A,且点A的横坐标为2,则
的图象有公共点A,且点A的横坐标为2,则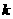 ( )
( )
A.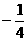 B.
B.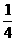 C .
C .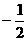 D.
D.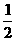
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com