
题目列表(包括答案和解析)
11、(1)若存在Q,则PA⊥面ABCD?AQ⊥QD
设BQ=x,则CQ=a-x
△ABQ∽△QCD 即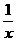 =
=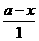 有解
有解
x2-ax+1=0(有解)
亦即Δ≥0,a2-4≥0,a≥2
(2)Δ=0即a=2时,x=1,Q为中点取AD中点H,过H作HG⊥PD于G,则GH∥CD,CH⊥AD,QH⊥面PA D
由三垂线定理QG⊥PD,∠QGH为所求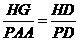
∴HG=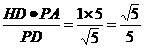
tan∠QGH=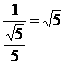
∠QGH=arctan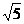
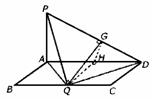
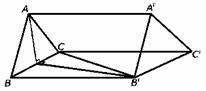
10、(1)过C′作C′G⊥面BAD于G,连结DG.
∵AD=BA=2 AD⊥AB
∴∠ADB=45°
又∵∠ADC=180°-45°=135°
∴∠BDC=135°-45°=90°
即BD⊥DC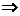 BD⊥DC′
BD⊥DC′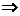 BG⊥BD ∴∠GDC′=60°
BG⊥BD ∴∠GDC′=60°
C′G为所求
C′G=C′D·sib60°=2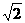 ·
·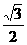 =
=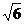
(2)DG=C′D·cos60°=2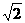 ·
·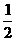 =
= 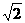 又AD=2 A到BD的距 离AO=AD·sin45°=2α×
又AD=2 A到BD的距 离AO=AD·sin45°=2α×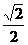 =
= 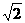
∴AG∥OD,即AG⊥DG,∠GAC′为所求.
tan∠GAC′=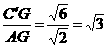
∴∠GAC′=60°
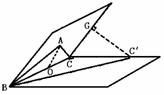
(1题图)
7、60°或120° 8、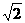 9、(1)(4)
9、(1)(4)
15、(1)取BC中点O,则AB=AC?AO⊥BC.BC′=CC′?C′O⊥BC.
∴BC⊥面AOC′?BC⊥AC′
(2)面BB′C′C⊥面ABC ∴AO⊥面BB′C′C C′O⊥底面ABC,面ABC∥面A′B′C′
∴OC′为两平面间的距离,OC′为所求.
∵BC=AC=AB=2 ∴CO=1 CC′=3 ∴OC′=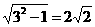
09F102
1-6、BCCCDD
14、取AB中点H,则HF∥AD∥A′D′,连结HB′交A′E于G.
又∵AD⊥面ABB′A′ ∴HF⊥HG ①
∵△HBB′≌△EB′A′∴∠HBE′+∠A′EB′=90°∴HG⊥A′E ②
HB⊥面A′B′E,HG为所求.
∴A′E=HB′=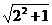 =
=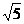 B′G=
B′G=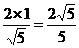 ∴HG=
∴HG=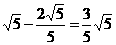
13、延长AO到E则AE⊥BC,又∵DO⊥面ABC,∴DE⊥BC ∠DEO=30° 又∵AO=a ∴OE=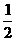 a DE=
a DE=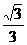 a BC=
a BC=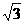 a ∴S△BDC=
a ∴S△BDC=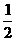 BC·DE=
BC·DE=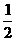 ·
·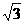 a×
a×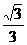 a =
a =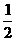 a
a
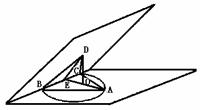
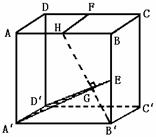
(13题图) (14题图)
9、8个 10、60° 11、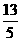 12、
12、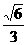
13、(1)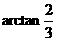 ; (2)
; (2)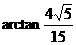 . (3)
. (3)
09F101
1-8、DDCD CCB
12.略
11、(1)略(2)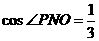
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com