
题目列表(包括答案和解析)
22、(本小题满分12分)
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
(1)当M在何处时,BC1//平面MB1A,并证明之;
 (2)在(1)下,求平面MB1A与平面ABC所成的二面角的大小;
(2)在(1)下,求平面MB1A与平面ABC所成的二面角的大小;
(3)求B-AB1M体积的最大值.
21、(本小题满分12分)
如图,梯形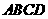 中,
中,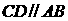 ,
,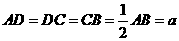 ,
,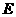 是
是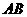 的中点,将
的中点,将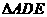 沿
沿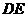 折起,使点
折起,使点 折到点
折到点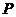 的位置,且二面角
的位置,且二面角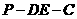 的大小为
的大小为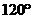
(1)求证: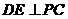 ;
;
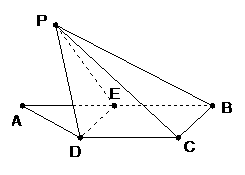 (2)求点
(2)求点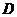 到平面
到平面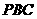 的距离;
的距离;
(3)求二面角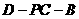 的大小.
的大小.
20、(本小题满分13分)
已知正四棱柱ABCD-A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点F为BD1中点.
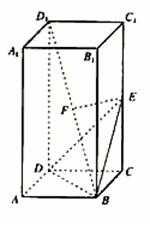 (1)证明EF为BD1与CC1的公垂线;
(1)证明EF为BD1与CC1的公垂线;
(2)求点D1到面BDE的距离.
19、(本小题满分13分)
4个男生,3个女生站成一排.(必须写出解析式再算出结果才能给分)
⑴ 3个女生必须排在一起,有多少种不同的排法?
⑵ 任何两女生彼此不相邻, 有多少种不同的排法?
⑶ 甲,乙二人之间恰好有三个人,有多少种不同的排法?
⑷ 甲,乙两生相邻,但都不与丙相邻,有多少种不同的排法?
18、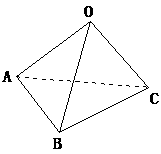 (本小题满分13分)
(本小题满分13分)
已知球面上的三点A、B、C,且AB=6,BC=8,AC=10,球O的半径R=13,求球心O到面ABC的距离。
17、(本小题满分13分)
已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=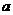 ,E、F是
,E、F是
侧棱PD、PC的中点。 (1)求证:EF∥平面PAB ;
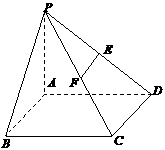 (2)求直线PC与底面ABCD所成角
(2)求直线PC与底面ABCD所成角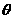 的正切值。
的正切值。
16、已知m、n是不同的直线,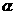 、
、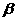 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
(1) 若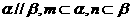 ,则
,则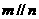 (2) 若
(2) 若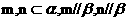 ,则
,则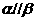 ;
;
(3) 若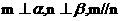 ,则
,则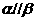 ;(4)
;(4)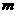 、
、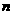 是一对异面直线且
是一对异面直线且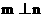 , 若
, 若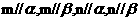 ,则
,则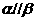 ,其中,真命题的编号是_____ (写出所有正确结论的编号).
,其中,真命题的编号是_____ (写出所有正确结论的编号).
15、表面积为4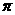 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积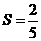 ,则球心到二面角的棱的距离为 _____ .
,则球心到二面角的棱的距离为 _____ .
14、正六棱锥S-ABCD的底面边长为6,侧棱长为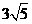 ,则它的侧面与底面所成的二面角的大小为_________.
,则它的侧面与底面所成的二面角的大小为_________.
13、正四面体V-ABC的棱长为2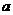 ,E,F,G,H分别是VA,VB,
,E,F,G,H分别是VA,VB,
BC,AC的中点,则四边形EFGH面积是________________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com