
题目列表(包括答案和解析)
7、正方体、等边圆柱(底面直径与高相等的圆柱)、球的体积相等时, 的表面积最小
班级 姓名
6、正方体的棱长为4,则正方体的外接球的面积为 ;内切球的面积为 ;
与正方体各棱相切的球的面积为 。
5、已知球O1的体积是球O2体积的125倍,球O1的半径是10㎝,则球O2的表面积
是 。
4、火星的半径是地球半径的一半,地球的表面积是火星的表面积的 倍。
3、设球内切于圆柱,则此圆柱的全面积与球的表面积之比为
A.1:1 B.2:1 C.3:2 D.4:3
2、球的表面积与它的内接正方体的表面积之比是
A、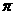 /3 B
/3 B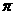 /4 C、
/4 C、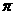 /2 D、
/2 D、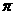
1、两个球的体积之比为8:27,那么这两个球的表面积的比为
A、2:3 B、4:9 C、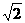 :
: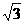 D、
D、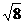 :
: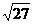
10、如图,有一轴截面为正三角形的倒圆锥形容器,内部盛水的高度为h,放入一个球后,水面恰好与球相切,求球的半径

广水一中高二数学同步练习09093
9、球半径为R,圆柱底面半径也为R,高为2R。从圆柱中挖去两个圆锥,它们都以圆柱的中截面的中心为顶点,又分别以圆柱的上、下底面为底面。球的体积与挖去圆锥后的圆柱剩余部分的体积之间有什么关系?请说明理由。
8、在半径为R的半球内有一内接圆柱,求这个圆柱侧面积的最大值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com