
题目列表(包括答案和解析)
8.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( )
A.16种 B.36种 C.42种 D.60种
7.若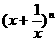 展开式的二项式系数之和为64,则展开式
展开式的二项式系数之和为64,则展开式
的常数项为( )
A.10 B.20 C.30 D.120
6.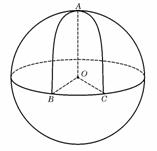 设球
设球 的半径是1,
的半径是1, 、
、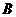 、
、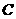 是球面上三点,已知
是球面上三点,已知 到
到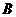 、
、
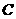 两点的球面距离都是
两点的球面距离都是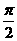 ,且二面角
,且二面角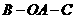 的大小是
的大小是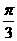 ,则
,则
从 点沿球面经
点沿球面经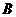 、
、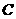 两点再回到
两点再回到 点的最短距离是( )
点的最短距离是( )
A.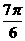 B.
B.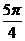 C.
C.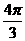 D.
D.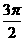
5.已知平面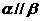 ,直线
,直线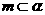 ,直线
,直线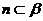 ,点
,点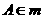 ,点
,点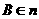 ,记点
,记点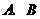 之间的距离为
之间的距离为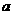 ,点
,点 到直线
到直线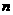 的距离为
的距离为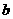 ,直线
,直线 和
和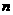 的距离为
的距离为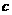 ,则( )
,则( )
A.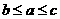 B.
B.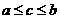 C.
C.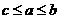 D.
D.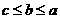
4. 给出下列四个命题:
①垂直于同一直线的两条直线互相平行;②垂直于同一平面的两个平面互相平行;③若直线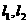 与同一平面所成的角相等,则
与同一平面所成的角相等,则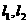 互相平行;④若直线
互相平行;④若直线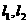 是异面直线,则与
是异面直线,则与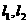 都相交的两条直线是异面直线.其中假命题的个数是( )
都相交的两条直线是异面直线.其中假命题的个数是( )
A.4 B.3 C.2 D.1
3.顶点在同一球面上的正四棱柱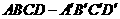 中,
中,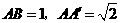 ,则
,则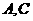 两点间的球面距离为( )
两点间的球面距离为( )
A.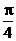 B.
B.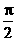 C.
C.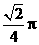 D.
D.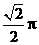
2.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( )
A.5部分 B.6部分 C.7部分 D.8部分
1. 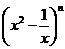 的展开式中,常数项为
的展开式中,常数项为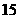 ,则
,则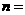 ( )
( )
A.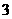 B.
B.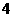 C.
C.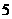 D.
D.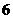
22.(本小题满分12分)
函数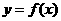 对任意实数
对任意实数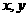 都有
都有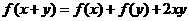 ,
,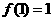
(Ⅰ)求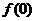 的值;
的值;
(Ⅱ)求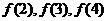 的值,猜想
的值,猜想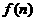 的表达式并用数学归纳法证明你的结论;
的表达式并用数学归纳法证明你的结论;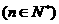
(Ⅲ)若数列{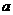
 },(n∈N
},(n∈N )是等差数列,则有数列{
)是等差数列,则有数列{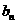 }(b
}(b =
=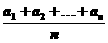 )
)
(n∈N )也是等差数列,类比上述性质,相应地:若数列{c
)也是等差数列,类比上述性质,相应地:若数列{c }是等比数列,且
}是等比数列,且
c >0(n∈N
>0(n∈N ),则有{
),则有{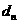 }(d
}(d
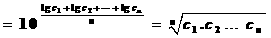 )(n∈N
)(n∈N )
)
也是等比数列.又类比上述性质,相应地:若数列{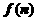 },(n∈N
},(n∈N )是“QQ”数列,
)是“QQ”数列,
则有数列{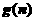 } (n∈N
} (n∈N )也是“QQ”数列.
写出一个数列
)也是“QQ”数列.
写出一个数列 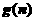 。
。
21. (本小题满分14分)
等差数列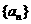 的前
的前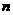 项和为
项和为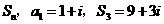 .(
.(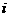 是虚数单位)
是虚数单位)
(Ⅰ)求数列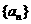 的通项
的通项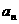 与前
与前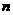 项和
项和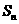 ;
;
(Ⅱ)设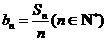 ,求证:数列
,求证:数列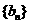 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com