
题目列表(包括答案和解析)
21、(12分)已知在三棱锥S-ABC中,底面是边长为4的正三角形,侧面SAC⊥底面ABC,M,N分别是AB,SB的中点,SA=SC=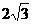 :
:
⑴求证AC⊥SB
⑵求二面角N-CM-B的大小
⑶求点B到面CMN的距离
20、(12分)在直三棱柱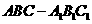 中,
中,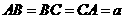 ,
,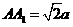 ,求
,求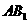 与侧面
与侧面 所成的角。
所成的角。
19、(12分)球面上三点A、B、C组成这个球的一个截面的内接三角形,AB=18,BC=24,AC=30,且球心到该截面的距离为球半径的一半。
(1)求球的表面积;
(2)求A,C两点的球面距离。
18、(12分)从{-3,-2,-1,0,1,2,3,}中任取3个不同的数作为抛物线方程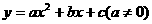 的系数,如果抛物线过原点且顶点在第一象限,则这样的抛物线有多少条?
的系数,如果抛物线过原点且顶点在第一象限,则这样的抛物线有多少条?
17、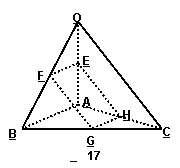 已知空间四边形
已知空间四边形 中,
中,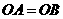 ,
,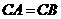 ,E、F、G、H分别为
,E、F、G、H分别为 、
、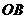 、
、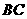 、
、 的中点,求证:四边形
的中点,求证:四边形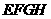 是矩形。(10分)
是矩形。(10分)
16、有两个相同的直三棱柱,高为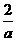 ,底面三角形的三边长为
,底面三角形的三边长为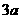 、
、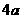 、
、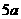 (
(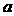 ﹥0).用它们拼接成一个三棱柱或者四棱柱,在所有可能的情形中,全面积最小的是四棱柱,则
﹥0).用它们拼接成一个三棱柱或者四棱柱,在所有可能的情形中,全面积最小的是四棱柱,则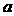 的取值范围是
的取值范围是
三:解答题(本大题共70分)
15、在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论)。①矩形;②不是矩形的平行四边形;③有三个面是等腰直角三角形,有一个面是等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体。
14、椭圆方程为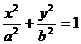 ,
,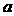 ,
,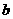
 {1,2,3,4,5,6},则焦点在
{1,2,3,4,5,6},则焦点在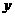 轴上的不同椭圆有
个。
轴上的不同椭圆有
个。
13、已知两异面直线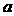 ,
,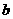 所成的角为
所成的角为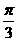 ,直线
,直线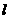 分别与
分别与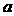 ,
,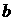
 所成的角都是
所成的角都是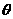 ,则
,则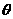 的取值范围是
。
的取值范围是
。
12、已知四棱锥P-ABCD的体积为V,AB∥CD,且AB:CD=2:3,点Q是PA的中点,则三棱锥Q-PBC的体积是( )
A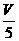 B
B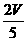 C
C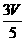 D
D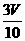
二:填空题(4×5=20分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com