
题目列表(包括答案和解析)
3.命题“若a²+b²=0,则a=0且b=0”的逆否命题是( )
(A)若a=0且b=0,则a²+b²=0 (B)若a≠0或b≠0,则a²+b²≠0
(C)若a²+b²≠0,则a≠0或b≠0 (D)若a≠0且b≠0,则a²+b²≠0
2.双曲线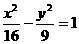 的渐近线方程为( )
的渐近线方程为( )
(A)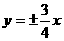 (B)
(B)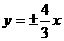 (C)
(C)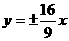 (D)
(D)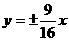
只有一项是符合题目要求的。
1.命题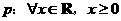 的否定是( )
的否定是( )
(A)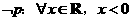 (B)
(B)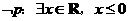
(C)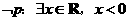 (D)
(D)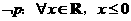
21. 甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为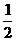 与
与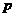 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为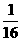 .
.
(Ⅰ)求乙投球的命中率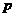 ;(用数字作答)
;(用数字作答)
(Ⅱ)求甲投球2次,至少命中1次的概率;(用数字作答)
(Ⅲ)若甲、乙两人各投球2次,求两人共命中2次的概率.(用数字作答)
20. 如图,正三棱柱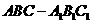 的所有棱长都为2,
的所有棱长都为2,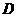 为
为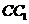 中点.
中点.
(Ⅰ)求证: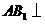 平面
平面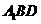 ;
;
(Ⅱ)求二面角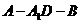 的大小;
的大小;
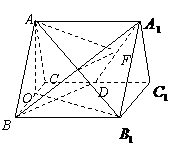 (Ⅲ)求点
(Ⅲ)求点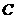 到平面
到平面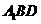 的距离.
的距离.
19. 正四棱柱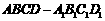 中,底面边长为
中,底面边长为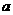 ,侧棱
,侧棱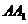 长为
长为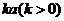 ,
,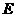 为侧棱
为侧棱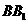 的中点,记以
的中点,记以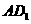 为棱,
为棱,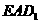 ,
,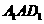 为面的二面角大小为
为面的二面角大小为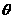 ,
,
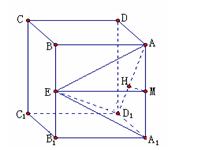 (1)是否存在
(1)是否存在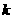 值,使直线
值,使直线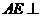 平面
平面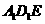 ,若存在,求出
,若存在,求出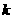 值;若不存在,说明理由;
值;若不存在,说明理由;
(2)试比较 与
与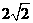 的大小。
的大小。
18. 某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;(用数字作答)
(II)任选3名下岗人员,求这3人中至少有2人参加过培训的概率.(用数字作答)
17.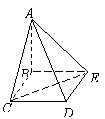 四棱锥
四棱锥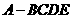 中,底面
中,底面 为矩形,侧面
为矩形,侧面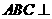 底面
底面 ,
,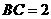 ,
,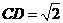 ,
,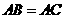 .
.
(Ⅰ)证明: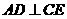 ;
;
(Ⅱ)设 与平面
与平面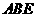 所成的角为
所成的角为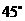 ,求二面角
,求二面角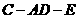 的大小.
的大小.
16. 有4个不同的球,4个不同的盒子,现在要把球全部放入盒内。
(1)共有多少种放法?(用数字作答)
(2)恰有一个盒不放球,有多少种放法?(用数字作答)
(3)恰有两个盒不放球,有多少种方法?(用数字作答)
15. 设a、b是不重合的两个平面,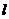 、m是不重合的两条直线,给出下列四个条件:
、m是不重合的两条直线,给出下列四个条件:
①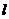 Ìa,mÌa,且
Ìa,mÌa,且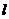 ∥b,m∥b
∥b,m∥b
②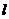 ^a,m^b,且
^a,m^b,且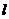 ∥m
∥m
③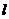 、m是相交直线,
、m是相交直线,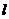 ∥a,m∥a,
∥a,m∥a,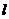 ∥b,m∥b
∥b,m∥b
④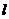 与a、b所成的角相等
与a、b所成的角相等
其中是a∥b的充分条件的有_____________个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com