
22.(本小题满分14分)
数轴上有一列点P1,P2,P3,…,Pn,…,已知当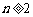 时,点Pn是把线段Pn – 1 Pn+1作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,Pn Pn + 1的长度分别为a1,a2,a3,…,an,其中a1 = 1.
时,点Pn是把线段Pn – 1 Pn+1作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,Pn Pn + 1的长度分别为a1,a2,a3,…,an,其中a1 = 1.
(1)写出a2,a3和an(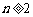 ,
,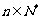 )的表达式;
)的表达式;
(2)证明a1 + a2 + a3 +…+an < 3(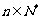 );
);
(3)设点Mn( n,an)(n > 2,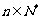 ),在这些点中是否存在两个点同时在函数
),在这些点中是否存在两个点同时在函数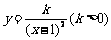 的图像上,如果存在,请求出点的坐标;如果不存在,请说明理由.
的图像上,如果存在,请求出点的坐标;如果不存在,请说明理由.
21.(本小题满分12分)
已知函数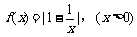 .
.
(1)当0 < a < b,且f ( a ) = f ( b )时,求证:ab>1;
(2)若存在实数a,b(a < b),使得函数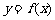 的定义域为 [a,b]时,值域为
的定义域为 [a,b]时,值域为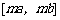 (
(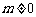 ),求m的取值范围.
),求m的取值范围.
20.(本小题满分14分)
已知圆C经过P(4,–
2),Q(– 1,3)两点,且在y轴上截得的线段长为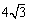 ,半径小于5.
,半径小于5.
(1)求直线PQ与圆C的方程.
(2)若直线l∥PQ,且l与圆C交于点A、B,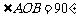 ,求直线l的方程.
,求直线l的方程.
19.(本小题满分12分)
数列{an}中,a1 = 1,当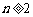 时,其前n项和满足
时,其前n项和满足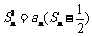
(1)求Sn的表达式;
(2)设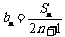 ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.
18.(本小题满分12分) 已知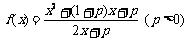
(1)若p > 1时,解关于x的不等式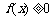 ;
;
(2)若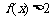 对
对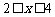 时恒成立,求p的范围.
时恒成立,求p的范围.
17.(本小题满分12分)
已知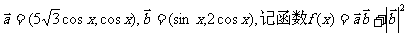
(1) 求函数f ( x )的最小正周期;
(2)
当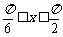 时,求函数f ( x )的值域.
时,求函数f ( x )的值域.
14.已知函数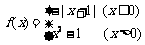 .那么不等式
.那么不等式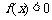 的解集为_______________.
的解集为_______________.
15.x、y满足约束条件: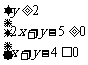 ,则
,则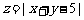 的最小值是______________.
的最小值是______________.
16对于函数f ( x ) = x | x | + px + q,现给出四个命题:
① q = 0时,f ( x )为奇函数
② y = f ( x )的图象关于(0,q)对称
③ p = 0,q > 0时,方程f ( x ) = 0有且只有一个实数根
④方程f ( x ) = 0至多有两个实数根
其中正确命题的序号为_____________________.
13.如图,某地一天从6时到14时的温度变化曲线近似满足函数
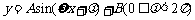 ,则温度变化曲线的函数解析式为____________.
,则温度变化曲线的函数解析式为____________.
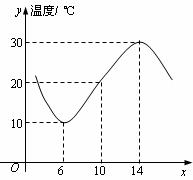
12.等差数列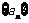 的前
的前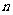 项和为
项和为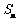 ,若
,若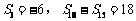 ,则
,则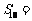 ____________.
____________.
11.若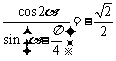 ,则
,则 的值为____________.
的值为____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com