
又p= ∴|
∴| |=4.
|=4.
 ,即|p-
,即|p-
(3)(文)由于抛物线y2=p(x+1)的焦点F坐标为(-1+ ,0),于是有
,0),于是有
由 得m>-2,m≠0;
得m>-2,m≠0;
∴p=f(m)= ,
,
即有x1x2+y1y2=0.
又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(
又p>0及
因此,直线与抛物线总有两个交点;
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),由(1)知,x1、x2是方程x2-(
∴x1+x2=
由OQ⊥OR,得kOQ?kOR=-1,
得x2-(
而判别式Δ=(
由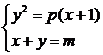
89.解:(1)抛物线y2=p(x+1)的准线方程是x=-1- ,直线x+y=m与x轴的交点为(m,0),由题设交点在准线右边,得m>-1-
,直线x+y=m与x轴的交点为(m,0),由题设交点在准线右边,得m>-1- ,即
,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com