
由 =4,解得k2=
=4,解得k2= ,∴k=±
,∴k=± .
.
∴△EPQ的面积为S△EPQ=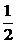 |PQ|?d=
|PQ|?d= .
.
d= .
.
|PQ|= |y1-y2|=
|y1-y2|= .
.
又点E到直线l的距离
故Δ= +16>0恒成立.
+16>0恒成立.
记这个方程的两实根为y1、y2,则
(2)解法一:设直线l的方程为y=k(x-2),因l与抛物线有两个交点,故k≠0,得x= +2,代入y2=4(x-1),得y2-
+2,代入y2=4(x-1),得y2- y-4=0,
y-4=0,
∴轨迹C的方程为x= +1,
+1,
即y2=4(x-1);
88.(1)解:设M点的坐标为(x,y),由点A的坐标为( .
.
xB=|BF|=|BN|=6.
设点P(x,y)是曲线段C上任一点,则由题意知P属于集合
{(x,y)|(x-xN)2+y2=x2,xA≤x≤xB,y>0}
故曲线段C的方程为y2=8(x-2)(3≤x≤6,y>0).
评述:本题考查根据所给条件选择适当的坐标系,求曲线方程的解析几何的基本思想,考查了抛物线的概念和性质、曲线和方程的关系以及综合运用知识的能力.
xN=|ME|+|EN|=|ME|+ =4
=4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com