
x轴上的椭圆,除去(0,0),(1,0),(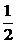 ,
, ),(
),(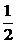 ,-
,- )四点.
)四点.
评述:第(Ⅰ)问是要求用解析的方法证明平面几何中的著名问题:三角形的重心、外心、垂心三心共线(欧拉线)且背景深刻,是有研究意义的题目.
因此,顶点C的轨迹是中心在(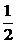 ,0),长半轴长为
,0),长半轴长为 ,短半轴长为
,短半轴长为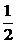 ,且短轴在
,且短轴在
即 =1(x≠
=1(x≠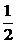 ,y≠0).
,y≠0).
 .
.
配方得3(b-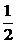 )2+c2=
)2+c2= ,即
,即
3(b2-b)+c2=0(c≠0,b≠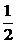 ),
),
(Ⅱ)解:若FH∥OB,由kFH= =0,得
=0,得
 ,
,
所以,kGH=kFG,G、F、H三点共线.
综上可得,G、F、H三点共线.
因为 ,
,
当b≠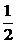 时,设G、H所在直线的斜率为kGH,F、G所在直线的斜率为kFG.
时,设G、H所在直线的斜率为kGH,F、G所在直线的斜率为kFG.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com