
得k=± ,α=
,α= 或
或 .
.
评述:本题考查直线与抛物线的位置关系,点的轨迹方程,直线的基础知识等.
∴ =4.
=4.
=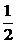
 .
.
∵S△EPQ=4,
=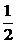 ?1?
?1?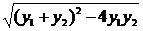
S△EPQ=S△EPD+S△EQD=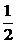 |ED|?(|y1|+|y2|)=
|ED|?(|y1|+|y2|)=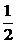 |ED|?|y1-y2|
|ED|?|y1-y2|
解法三:设直线l的方程为y=k(x-2),因为直线与抛物线交于两点,所以k≠0,则x= +2,代入y2=4(x-1)得y2-
+2,代入y2=4(x-1)得y2- y-4=0.
y-4=0.
所以|PQ|=x1+x2= .
.
其余同解法一.
记这个方程的两个实根为x1、x2,因抛物线y2=4(x-1)的焦点是D(2,0),准线是x=0.
k2x2-(4k2+4)x+4k2+4=0.
因直线l与抛物线有两个交点,故k≠0,
而Δ=16(k2+1)>0恒成立.
∴α= 或α=
或α= .
.
解法二:设直线l的方程为y=k(x-2),代入y2=4(x-1),得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com