故△ABP的面积函数S（a）的值域为（0，）.

即a＞，得0＜＜1，于是0＜S（a）＜

∵a＞b＞0，b=，∴a＞，

∴S（a）=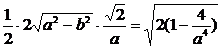

（Ⅱ）解：∵在△ABP中，|AB|=2，高为，

故P的坐标为（）.

解得  （舍去）

85.（Ⅰ）解：将y=代入椭圆方程，得，

化简得  b²x⁴－a²b²x²+a²=0，

由条件，有Δ=a⁴b⁴－4a²b²=0

得ab=2

∴（1+a）

整理得：（1－a）x²－2ax+（1+a）y²=0（0＜x＜a）

（Ⅱ）当|BD|=0时，∠BOA=π，则点C的坐标为（0，0），满足上式

综合（Ⅰ）（Ⅱ），得点C的轨迹方程为

（1－a）x²－2ax+（1+a）y²=0（0≤x＜a）.

以下同解法一.

评述：本题主要考查了曲线与方程，直线和圆锥曲线等基础知识以及求动点轨迹的基本技能和综合运用数学知识解决问题的能力.解法一利用设点法引入参数b，消参数得方程.解法二则利用角之间关系，使用二倍角公式得出等式，化简较简捷，但分析时不容易想.

tanBOD=（1+a）