Δ＝4m²k²－4（k²－1）（m²－2）＝4（－2＋2k²）＝8k（3k－2）．

由方程组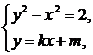

消去y，得（k²－1）x²＋2mkx＋m²－2＝0，

因为k²≠1，所以

因为直线l′在直线l的上方，所以M＝（k）．

解得m＝（k）．

可知．

由l上的点A到l′的距离为，

（3）当0≤k＜1时，双曲线S的上支在直线l的上方，所以B在直线l的上方，设直线l′与直线l：y＝k（x－）平行，两线间的距离为，且直线l′在直线l的上方，双曲线S的上支上有且仅有一个点B到直线l的距离为，等价于直线l′与双曲线S的上支有且只有一个公共点.

设l′的方程为y=kx+m

解得x＝，y＝2，即B（，2）

（2）设B（x，）是双曲线S到直线l：y＝x－的距离为的点，由点到直线距离公式有．

双曲线S的方程为＝1