2. 求由抛物线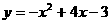与其在点A(1,0)和点B(3,0)处的切线所围成图形的面积。

1.已知函数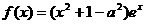 (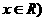，其中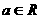

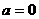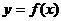(1)当时，求曲线在点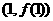处的切线的斜率；

(2)求函数的单调区间与极值。

5. 一名学生从他的家到学校的途中有6个交通岗，假设他在各交通岗遇到红灯的事件是独立的，并且概率都是1／3，求这名学生在途中遇到红灯数ξ的期望　　　　 与方差

4. 用数字0，1，2，3，4，5组成没有重复数字的四位数，其中个位、十位、和百位上的数字之和为偶数的四位数共有　　　　　 个(用数字作答)。

3. 计算：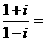　　　　 　　　

2. 甲、乙两人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙两人依次各抽一题．两人中至少有一个抽到选择题的概率是　　　　　　

1. 现有6张同排连座号的电影票, 分给3名老师与3名学生, 要求师生相间而坐, 则不同的分法数为___________

21．　 (12分) 等比数列{a_n}的前n项和为S_n，已知对任意的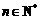，点(n，S_n)均在函数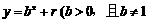，b、r均为常数)的图象上．

(1)　　 求r的值；

(2)　　 当b = 2时，记．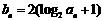

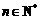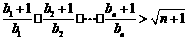证明：对任意，不等式成立．

(命题人：郑莹莹　　 审题人：周先凤)

西南师大附中2008-2009学年度下期期末考试

20．　 (12分) 某社区文化站举行一次象棋比赛，经优胜劣汰，最后由甲、乙二人决赛．根据他们过去比赛的情况统计知，单局比赛甲胜乙的概率为0.6．本次比赛采用五局三胜制，即先胜三局者获胜．设各局比赛相互间没有影响．求：

(1)　　 前三局甲领先的概率；

(2)　　 本场比赛乙以3∶2取胜的概率；

(3)　　 令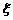为本场比赛的局数，求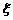的分布列和数学期望．

19．　 (12分) 如图，在直三棱柱ABC-A₁B₁C₁中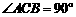，，AC = BC = CC₁ = 2．

(1)　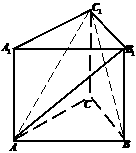　 求证：AB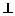₁BC₁；

(2)　　 求点B到平面AB₁C₁的距离；

(3)　　 求二面角C­₁-AB₁-A₁的大小．