22.(14分)设数列{a_n}的前n项和为S_n，且a₁=1，S_n+1=4a_n+2(n∈N^*)。

(1)设b_n=a_n+1-2a_n，求证：数列{b_n}是等比数列

(2)求数列{a_n}的通项公式；

(3)求S_n.

21.(12分)若数列{a_n}是等比数列，a_n﹥0，公比q≠1，已知lga₂是lga₁和1+lga₄的等差中项，且a₁a₂a₃=1.

(1)求{a_n}的通项公式；

(2)设b_n=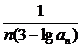(n∈N^*)，求其前n项和。

20.(12分)已知圆x²+y²+x-6y+m=0，直线L过点(1，1)，若被x轴反射可经过点(5，1)，又直线L与此圆相交于A、B两点，且OA⊥OB(O为坐标原点),

(1)求m的值

(2)点P(a,b)在圆上，求a²+b²的最大值。

19．(12分)如图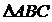，和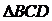是两副三角板，它们所在的平面互相垂直，且AB=AC, ==，=,

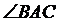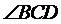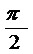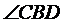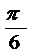(1)求证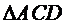：和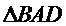都是直角三角形；

(2)求直线BC与平面ACD所成角的大小；

(3)若AB=1，求四面体的体积。

18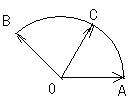．(12分)给定两个长度为1的平面向量OA和OB，它们的夹角为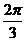，如图所示，点C在以O为圆心的圆弧AB上变动。若OC=xOA+yOB,其中x,y∈R，求x+y的最大值。

17.(12分)已知a=(sinx,-cosx),b=(sinx,sinx),c=(cosx,-cosx),x∈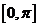,f(x)=a(b+3c),求f(x)的单调区间和值域。

16.若圆x²+y²-4x-4y-10=0上至少有三个不同点到直线l：ax+by=0的距离为2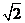，则直线l的倾斜角范围是　　　　　 。

15．实数x满足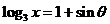，则=　 　　　.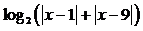

14. 已知直线L过点P(2.1)且于X轴,Y轴正半轴分别交于点A,B,则三角形ABO(O为坐标原点)面积的最小值为　　　　　 。

13. 设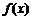是偶函数，其定义域为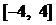，且在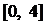内是增函数，又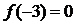，则不等式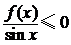的解集为　　　　　　　 。