
题目列表(包括答案和解析)
4.
函数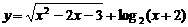 的定义域为( )
的定义域为( )
A. B.
B.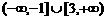 C.
C.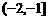 D.
D.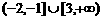
3.
若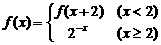 ,则
,则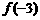 的值为( )
的值为( )
A.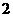 B.
B.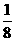 C.
C.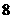 D.
D.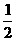
2.
已知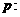 不等式
不等式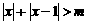 的解集为
的解集为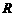 ,
,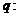
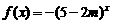 是减函数,则
是减函数,则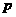 是
是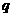 的( )
的( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也不必要条件
1.
若集合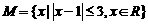 ,
,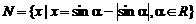 ,则
,则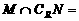 ( )
( )
A.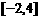 B.
B.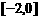 C.
C.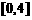 D.
D.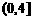
22. (本小题满分14分)
已知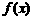 在
在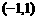 上有定义,
上有定义,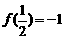 ,且满足
,且满足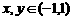 有
有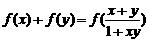
(Ⅰ)证明: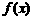 在
在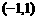 上为奇函数;
上为奇函数;
(Ⅱ)对数列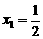 ,
,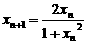 ,求
,求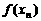 ;
;
(Ⅲ)求证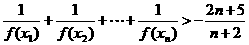
21. (本小题满分12分)
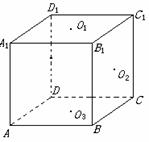 如图,正方体
如图,正方体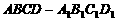 中,
中,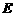 为
为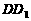 的中点,
的中点,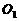 ,
,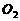 ,
,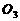 分别为面
分别为面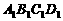 ,面
,面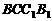 ,面
,面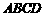 的中心。(1)求证:
的中心。(1)求证: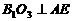 ;(2)求异面直线
;(2)求异面直线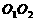 与
与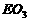 所成的角。
所成的角。
20. (本小题满分12分)
已知函数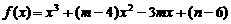 (
(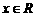 )的图象关于原点对称,
)的图象关于原点对称, ,
,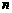 为实常数。(1)求
为实常数。(1)求 ,
,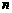 的值;(2)试用单调性定义证明
的值;(2)试用单调性定义证明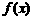 在区间
在区间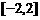 上是单调函数;(3)当
上是单调函数;(3)当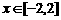 时,不等式
时,不等式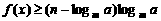 恒成立,求实数
恒成立,求实数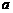 的取值范围。
的取值范围。
19. (本小题满分12分)
某蛋糕厂生产某种蛋糕的成本为40
元/个,出厂价为60元/,日销售量1000个,为适应市场需求,计划提高蛋糕档次,适度增加成本,若每个蛋糕成本增加的百分率为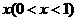 ,则每个蛋糕的出厂价相应提高的百分率为
,则每个蛋糕的出厂价相应提高的百分率为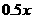 ,同时预计日销售量增加的的百分率为
,同时预计日销售量增加的的百分率为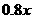 ,已知: 日利润= (出厂价-成本)
,已知: 日利润= (出厂价-成本)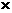 日销售量 ,且设增加成本后的日利润为
日销售量 ,且设增加成本后的日利润为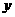 .
.
(1)写出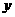 与
与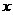 的函数关系:
的函数关系:
(2)为使日利润有所增加,问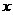 应在什么范围内?
应在什么范围内?
18. (本小题满分12分)
设命题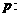 函数
函数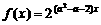 是减函数;命题
是减函数;命题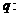 不等式
不等式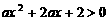 的解集为
的解集为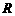 ,如果
,如果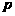 且
且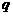 为假命题,
为假命题,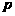 或
或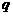 为真命题,求
为真命题,求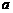 的取值范围。
的取值范围。
17. (本小题满分12分)
已知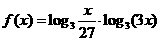 ,当
,当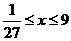 时,求
时,求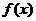 的最大值和最小值及相应的
的最大值和最小值及相应的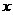 的值 .
的值 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com