
题目列表(包括答案和解析)
3.设{an}是正项等比数列,且a5a6=10,则lga1+lga2+…+lga9+lga10等于
A.5 B.l+lg5 C.2 D.10
2.若p、q为简单命题,则“p且q为假”是“p或q为假”的
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
1.tan(- )的值是
)的值是
A.-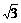 B.-
B.-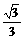 C.
C.
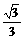 D.
D.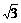
(17)(本小题满分12分):
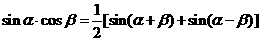
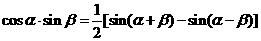
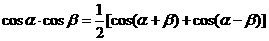
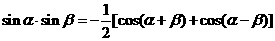
已知复数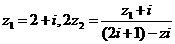 。
。
(Ⅰ)求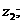
(Ⅱ)若△ABC的三个有A、B、C依次成等差数列,且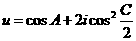 ,求
,求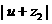 的取值范围。
的取值范围。
(18)(本小题满分12分)
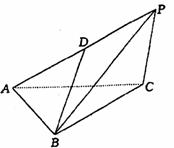
三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P―AC―B为120°,PC=2,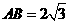 。
。
(Ⅰ)求证: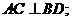
(Ⅱ)求BD与底面ABC所成角的正弦值;
(Ⅲ)求三棱锥P-ABC的体积。
(19)(本小题满分12分)
某公司年初有资金500万元,由于坚持改革、大胆创新,每年资金递增20%,但该公司不忘回报社会,每年年底资助希望工程40万元,若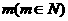 年后,该公司资金至少翻一番,求m的最小值。
年后,该公司资金至少翻一番,求m的最小值。
(参考数据: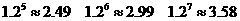 )
)
(20)(本小题满分12分)
设常数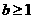 ,若
,若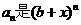 展开式中x的系数
展开式中x的系数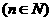 ,
,
(Ⅰ)写出数列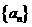 的通项公式;
的通项公式;
(Ⅱ)设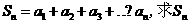 ;
;
(Ⅲ)当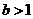 时,求
时,求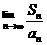 的值。
的值。
(21)(本小题满分12分)
(文)若函数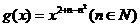 ,满足
,满足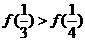 。
。
(Ⅰ)求n的值;
(Ⅱ)是否存在实数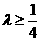 ,使函数
,使函数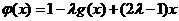 在区间
在区间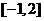 上的值域
上的值域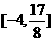 ,若存在,求出这个值,若不存在,说明理由。
,若存在,求出这个值,若不存在,说明理由。
(理)设 是定义在自然数集N上的函数,满足
是定义在自然数集N上的函数,满足 ,且对任意
,且对任意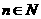 都有
都有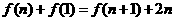 的成立。
的成立。
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)若函数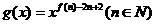 ,满足
,满足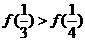 ,问是否存在实数
,问是否存在实数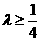 使函数
使函数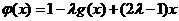 在区间
在区间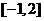 上的值域
上的值域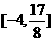 ,若存在,求出这个值,若不存在,说明理由。
,若存在,求出这个值,若不存在,说明理由。
(22)(本小题满发14分)
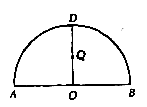
如图,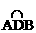 为半圆,AB为半圆直径,O为半圆圆心,且
为半圆,AB为半圆直径,O为半圆圆心,且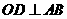 ,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。
,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线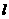 与曲线C相交于不同的M、N,且M在D、N之间设
与曲线C相交于不同的M、N,且M在D、N之间设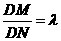 ,求λ的取值范围。
,求λ的取值范围。
(Ⅲ)(只理科做)过D的直线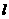 与曲线C相交于不同的两点M、N,求△OMN面积的最大值。
与曲线C相交于不同的两点M、N,求△OMN面积的最大值。
(13)若函数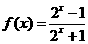 ,则
,则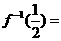 ______________ 。
______________ 。
(14)抛物线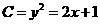 向右平移
向右平移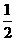 个单位得一曲线
个单位得一曲线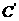 ,再把
,再把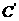 绕其项点逆时针旋转90°,则所得曲线方程为______________________
。
绕其项点逆时针旋转90°,则所得曲线方程为______________________
。
(15)当x =3时,不等式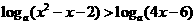 (a为常数,
(a为常数,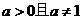 )成立,则此不等式的解集是_________________________ 。
)成立,则此不等式的解集是_________________________ 。
(16)把底面半么为8圆锥放倒在平面内,使圆锥在此平面内绕顶点O滚动,当这圆锥在以虚线所示的圆O上绕O点滚动一周而回到原处时,圆锥本身滚动了两周半,则圆锥的母线长为___________________ 。
(1)已知集合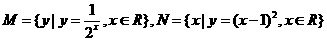 ,则集合M与N的关系为
( )
,则集合M与N的关系为
( )
(A)M=N
(B)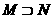
(C)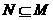 (D)
(D)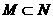
(2)下列函数中既是在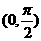 上是增函数,又是以
上是增函数,又是以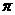 为周期的偶函数的是
( )
为周期的偶函数的是
( )
(A)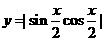 (B)
(B)
(C)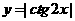 (D)
(D)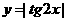
(3)(文)若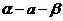 是直二面角,直线
是直二面角,直线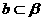 且b与a不重合,则
且b与a不重合,则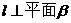 的一个充分但不必要条件是
( )
的一个充分但不必要条件是
( )
(A)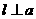 ,
,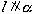 (B)
(B)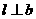 且
且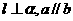
(C)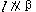 ,
,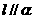 (D)
(D)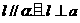
(理)复数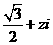 对应的向量按逆时针方向旋转120°后得到的向量对应的复数
对应的向量按逆时针方向旋转120°后得到的向量对应的复数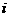 ,则复数z等于
( )
,则复数z等于
( )
(A)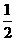 (B)
(B)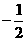
(C) (D)
(D)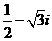
(4)(文)同(理)第3题
(理)已知双曲线的两条渐近线方程分别为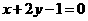 和
和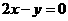 ,则该双曲线离心率为
( )
,则该双曲线离心率为
( )
(A)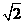 (B)
(B)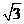
(C)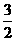 (D)
(D)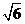
(5)同(理)第4题
(理)在空间四边形ABCD中,E、F分别为AB、CD的中点,若AD=BC,且AD与BC成60°角,则异面直线EF和BC所成角的大小为 ( )
(A)30° (B)60° (C)30°或60° (D)90°
(6)(文)同(理)第5题
(理)函数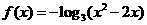 的单调递增减区间为
( )
的单调递增减区间为
( )
(A)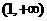 (B)
(B)
(C)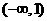 (D)
(D)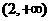
(7)(文)同(理)第6题
(理)有六支足球队争夺一次比赛的前四名,并对前四名发给不同的奖品,A、B是六支球的两支,若A、B不都获奖,则不同的发奖方式共有 ( )
(A)144种 (B)216种
(C)366种 (D)360种
(8)(文)同(理)第7题
(理)极坐标系中,直线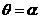 和直线
和直线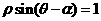 的位置关系是
( )
的位置关系是
( )
(A)垂直 (B)平行
(C)相关但不垂直愿 (D)相交
(9)(文)设实数x,y满足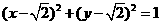 ,则
,则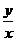 的最小值为
( )
的最小值为
( )
(A)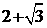 (B)
(B)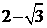
(C)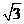 (D)
(D)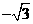
(理)若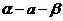 是直二面角,直线
是直二面角,直线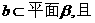 b与a不得合,则直线
b与a不得合,则直线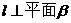 的一个充分但不必要条件是
( )
的一个充分但不必要条件是
( )
(A)(A)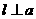 ,
,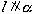 (B)
(B)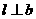 且
且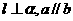
(C)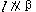 ,
,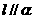 (D)
(D)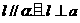
(10)已知一等差数列的前四项的和为124,后四项的和为156,又各项的和为210,则此等差数列共有 ( )
(A)8项 (B)7项
(C)6项 (D)5项
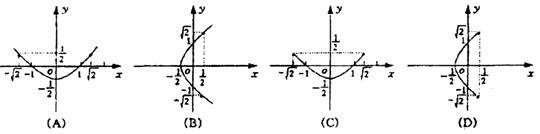
(11)已知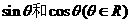 是方程
是方程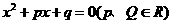 的两根,则动点(p,q)的轨迹图形是
( )
的两根,则动点(p,q)的轨迹图形是
( )
(12)商店某种贷物进价下降了8%,但销售价没有变,于是这种贷物的销售利润率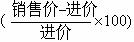 由原来的r %增加(r+10)%,,则r的值等于
( )
由原来的r %增加(r+10)%,,则r的值等于
( )
(A)12 (B)15 (C)20 (D)25
第Ⅱ卷 (非选择题 共90分)
20.(本小题满分14分)
已知:椭圆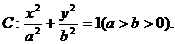
(Ⅰ)若点P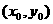 是椭圆C内部一点,求证:
是椭圆C内部一点,求证: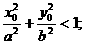
(Ⅱ)若椭圆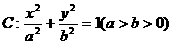 上存在不同的两点关于直线
上存在不同的两点关于直线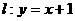 对称,试求
对称,试求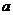 、
、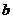 满足的关系式.
满足的关系式.
朝 阳 区 高 三 统 一 练 习(二)
19.(本小题满分14分)
已知:函数 在(-1,1)上有定义,
在(-1,1)上有定义,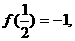 且满足
且满足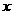 、
、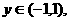 有
有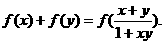
(Ⅰ)求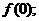
(Ⅱ)证明 在
在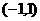 上为奇函数;
上为奇函数;
(Ⅲ)在数列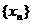 中,
中,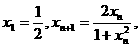 求f(xn)
求f(xn)
18.(本小题满分14分)
2002年底某县的绿化面积只占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
(Ⅰ)设该县的总面积为1,2002年底绿化面积为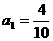 ,经过
,经过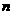 年后绿化的面积为
年后绿化的面积为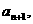 求证:
求证: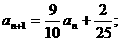
(Ⅱ)求数列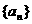 的第
的第 项
项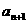 ;
;
(Ⅲ)至少需要多少年的努力,才能使绿化率超过60%.(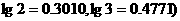
17.(本小题满分14分)
在三棱台ABC-A1B1C1中,侧棱A1A⊥底面ABC,且AC=BC1=2A1C1,
∠BAC=∠BC1C=90°.
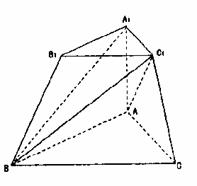 (Ⅰ)求证:CC1⊥平面ABC1;
(Ⅰ)求证:CC1⊥平面ABC1;
(Ⅱ)求AC与BC1所成的角;
(Ⅲ)若A1C1=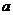 ,求AA1的长.
,求AA1的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com