
题目列表(包括答案和解析)
22.(本小题满分14分)在平面直角坐标系中, 为坐标原点,点
为坐标原点,点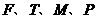 满足
满足
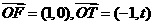 ,
,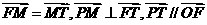
(I)当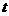 变化时,求点
变化时,求点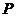 的轨迹
的轨迹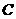 的方程;
的方程;
(II)若过点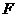 的直线交曲线
的直线交曲线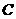 于
于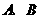 两点,求证:直线
两点,求证:直线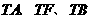 的斜率依次成
的斜率依次成
21.
(本小题满分12分)已知函数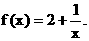 数列
数列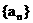 中,
中, 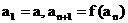
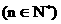 . 当a取不同的值时,得到不同的数列
. 当a取不同的值时,得到不同的数列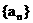 , 如当
, 如当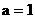 时, 得到无穷数列
时, 得到无穷数列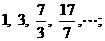 当
当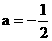 时, 得到有穷数列
时, 得到有穷数列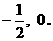
(I) 求a的值, 使得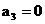 ;
;
(II) 设数列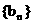 满足
满足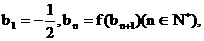
求证: 不论a取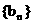 中的任何数, 都可以得到一个有穷数列
中的任何数, 都可以得到一个有穷数列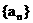 ;
;
(III) 求a的取值范围, 使得当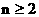 时, 都有
时, 都有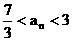 .
.
20.(本小题满分12分)已知函数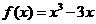 ,
,
(I)求函数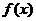 在
在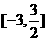 上的最大值和最小值;
上的最大值和最小值;
(II)过点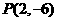 作曲线
作曲线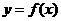 的切线,求此切线的方程.
的切线,求此切线的方程.
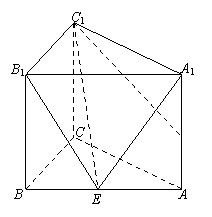
19.(本小题满分12分)如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等
腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
(Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);
(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;
(Ⅲ)在(Ⅱ)的条件下,求点D到平面B1C1E的距离.
18.(本小题满分12分)一位学生每天骑自行车上学, 从他家到学校有5个交通岗, 假设他在
交通岗遇到红灯是相互独立的, 且首末两个交通岗遇到红灯的概率均为p , 其余3个交通
岗遇到红灯的概率均为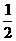 .
.
(I) 若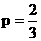 , 求该学生在第三个交通岗第一次遇到红灯的概率;
, 求该学生在第三个交通岗第一次遇到红灯的概率;
(II) 若该学生至多遇到一次红灯的概率不超过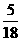 , 求p的取值范围.
, 求p的取值范围.
17.(本小题满分12分)在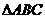 中,
中,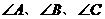 所对的边长分别为
所对的边长分别为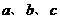 ,设
,设
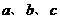 满足条件
满足条件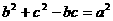 和
和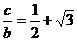 ,求
,求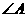 和
和 的值.
的值.
16.已知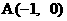 ,
, 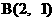 ,
, 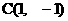 . 若将坐标平面沿x轴折成直二面角, 则折后
. 若将坐标平面沿x轴折成直二面角, 则折后
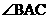 的余弦值为
.
的余弦值为
.
15.已知凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间内的任意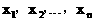 ,有
,有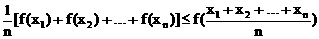 ,已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为
.
,已知y=sinx在区间(0,π)上是凸函数,那么在△ABC中,sinA+sinB+sinC的最大值为
.
14.给出下面的3个命题:(1)函数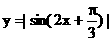 的最小正周期是
的最小正周期是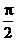 ;(2)函数
;(2)函数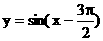 在区间
在区间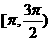 上单调递增;(3)
上单调递增;(3)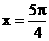 是函数
是函数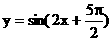 的图象的一条对称轴.其中正确命题的序号是
.
的图象的一条对称轴.其中正确命题的序号是
.
13.某中学的一个研究性学习小组共有10名同学,其中男生x名(3≤x≤9),现在从中选出
3人参加一次调查活动,若至少有1名女生去参加的概率为p,则p的最大值为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com