
题目列表(包括答案和解析)
20.(本小题满分12分)
已知函数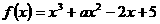

⑴若函数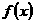 在
在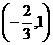 上单调递减,在
上单调递减,在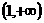 上单调递增,求实数
上单调递增,求实数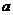 的值;
的值;
⑵求证:当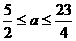 时,
时,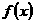 在
在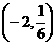 上单调递减
上单调递减
19.(本小题满分12分)
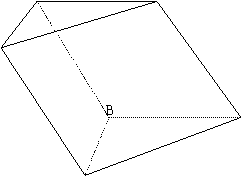
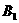
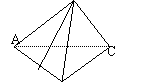
 已知三棱锥
已知三棱锥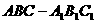 中,
中,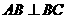 ,四边形
,四边形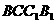 是矩形,四边形
是矩形,四边形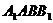 是菱形且
是菱形且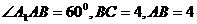

 ⑴求证:平面
⑴求证:平面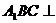 平面
平面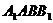 ;
;
⑵求直线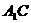 与平面
与平面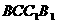 所成角的正切
所成角的正切
|
|
18.(本小题满分12分)
有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机投掷一次,所得点数较大者获胜
⑴分别求出两只骰子投掷所得点数的分布列及期望;
⑵投掷蓝色骰子者获胜的概率是多少?
三 解答题:本大题共6小题,共74分
解答题:本大题共6小题,共74分 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤
17.(本小题满分12分)
已知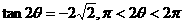
 求:
求:
⑴ ;
;
⑵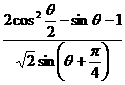

绝密★启用前
2005年10月济南市高三统一考试
数 学(理工类)
第Ⅱ卷(非选择题 共90分)
⒈第Ⅱ卷共6页,用钢笔或圆珠笔直接写在试题卷中
⒉答卷前将密封线内的项目填写清楚
二 填空题:本大题共4个小题
填空题:本大题共4个小题 每小题4分;共16分,把答案填在题中横线上
每小题4分;共16分,把答案填在题中横线上
|
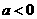 ,则关于
,则关于 不等式
不等式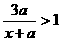 的解是
的解是

 ⒕在正三棱锥
⒕在正三棱锥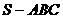 中,
中,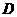 为
为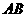 中点,且
中点,且
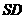 与
与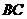 所成角为
所成角为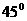 ,则
,则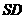 与底面
与底面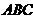
|
|

⒖已知椭圆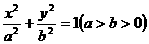 ,以原点为顶点,椭圆焦点
,以原点为顶点,椭圆焦点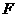 为焦点的抛物线
为焦点的抛物线
与椭圆相交与点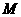 且
且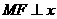 轴,则椭圆的离心率为
轴,则椭圆的离心率为

⒗下列结论中是真命题的有
(填上所有命题的序号)
①“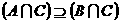 ”是“
”是“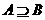 ”的必要不充分条件;②向量
”的必要不充分条件;②向量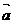 与向量
与向量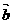 共
共
线,向量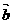 与向量
与向量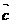 共线,则向量
共线,则向量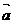 与向量
与向量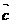 共线;③函数
共线;③函数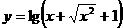 是
是
奇函数;④函数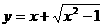 与函数
与函数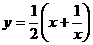 互为反函数
互为反函数
⒎函数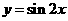 的图像按向量
的图像按向量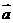 平移后,所得函数的解析式是
平移后,所得函数的解析式是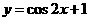 ,则
,则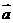 等于
等于
A
 B
B
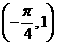 C
C
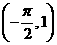 D
D
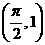
⒏下列函数在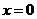 连续的是
连续的是
A
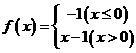 B
B
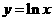
C
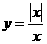 D
D
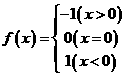
⒐下列命题中不正确的是(其中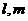 表示直线,
表示直线,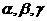 表示平面)
表示平面)
A
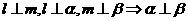 B
B

C
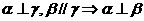 D
D

⒑某文艺团体下基层进行宣传演出,原准备的节目表中有6个节目,如果保持这些节目的
相对顺序不变,在它们之间再插入2个小品节目,并且这2个小品节目在节目表中既不
排头,也不排尾,则不同的插入方法有
A 20种 B
20种 B 30种 C
30种 C 42种 D
42种 D 56种
56种
⒒若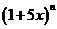 的展开式中各项二项式系数之和为
的展开式中各项二项式系数之和为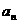 ,
,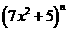 的展开式中各项系数之和为
的展开式中各项系数之和为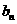 ,则
,则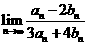 的值为
的值为
A
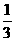 B
B -
-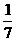 C
C
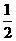 D
D -
-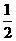
⒓已知点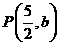 为椭圆
为椭圆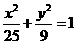 上的点,
上的点,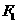

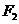 是椭圆的左
是椭圆的左 右焦点,
右焦点,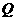 在线段
在线段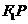 上,且
上,且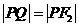 ,那么点
,那么点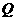 分有向线段
分有向线段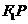 的比是
的比是
A 3:4 B
3:4 B 4:3 C
4:3 C 2:5 D
2:5 D 5:2
5:2
22.(本小题满分14分)
(理)已知正项数列{an}满足a1=a(0 a
a 1)且f(x)=
1)且f(x)=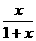 又an+1
又an+1 f(an)(n
f(an)(n 1且n
1且n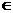 N)求证:
N)求证:
(1)an
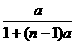
(2)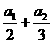 +…+
+…+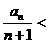 1
1
(文)已知数列{an},a1=1,前n项和为Sn,对于任意的n 2,n
2,n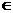 N+,Sn-1-8,an,8Sn-4恒为等差数列
N+,Sn-1-8,an,8Sn-4恒为等差数列
(1)求a2,a3,a4
(2)证明:在n 2时,数列{an}为等比数列。
2时,数列{an}为等比数列。
21.(本小题满分12分)
设f(x)=loga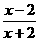 的定义域为[m,n],值域为[logaa(n-1),logaa(m-1)]
的定义域为[m,n],值域为[logaa(n-1),logaa(m-1)]
(1)求证:m 2
2
(2)求实数a的取值范围
20.(本小题满分12分)
已知f(n)=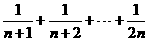 ,且不等式f(n)
,且不等式f(n)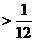 loga(a-1)+
loga(a-1)+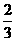 ,对一切大于1的自然数n成立,求实数a的范围。
,对一切大于1的自然数n成立,求实数a的范围。
19.(本小题满分12分)
已知二次函数f(x)的二次项系数为a,且不等式f(x) -2x的解集为(1,3)。
-2x的解集为(1,3)。
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式。
(2)若f(x)的最大值为正数,求a的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com