
题目列表(包括答案和解析)
2. 含参的二次函数的值域、最值
(1) 求a, 使函数y=2x2+5ax+2a的图象的顶点最高.
(2) m为何值时, 二次函数y=x(2m-3x)+4m的顶点位置最低?
(3) 设y=x2+px+q的最小值为0, 求q.
(4) 已知y=x2+2x+a,x∈[-3,2]最大值为4, 求a的值.
(5) 已知y=x2+2ax+1,x∈[-1,2]最大值为4, 求a的值.
(6) 已知y=ax2+2ax+1,x∈[-3,2]最大值为4, 求a的值.
(7) 巳知y=4mx2-2x+1,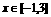 最小值为7, 求m的值.
最小值为7, 求m的值.
(8) 设y=x(2a-x),x∈[0,2]最大值为a2,求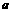 的取值范围.
的取值范围.
(9) 求函数y=2msinx-cos2x的最大值.
(10)若函数y=asin2x+2cosx-a-2(a∈R)的最小值为m, 求m的表达式.
(11)当函数y=sin2x+acosx+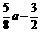 (0≤x≤
(0≤x≤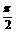 )取最大值1, 求a.
)取最大值1, 求a.
(12)设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a). ①用a写出的f(a)表达式. ②试确定能使f(a)=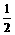 的a, 并对这个a, 求y的最小值.
的a, 并对这个a, 求y的最小值.
(13)已知函数y=x2-2x,x∈[t,t+1],求函数在[t,t+1]上取最小值.
(14)设y=-x2-4x+1,x∈[t-1,t+1], 试写出函数在[t-1,t+1]上的最大值.
(15)设函数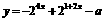 的最大值为3,求a的值.
的最大值为3,求a的值.
(16) 设A为曲线
设A为曲线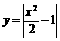 上任意一点, B(0, b)(b≥0)为y轴上一点, 求|AB|的最小值。
上任意一点, B(0, b)(b≥0)为y轴上一点, 求|AB|的最小值。
(17) 在长、宽分别是a(a>1), 1的矩形中, 截得平行四边形ABCD,
求平行四边形ABCD面积的最大值。
(18) 已知a,b∈R+,a≠b, ,
,
求m.
(19) 0<a<1,x,y满足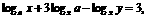 如果
如果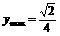 ,求a.
,求a.
(20) 求函数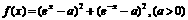 的最小值.
的最小值.
(21) 已知函数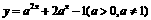 在区间[-1,1]上的最大值是14,求
在区间[-1,1]上的最大值是14,求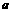 .
.
(22) 已知椭圆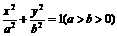 ,B是短轴上一个端点, P是椭圆上一动点, 求|PB|最大值.
,B是短轴上一个端点, P是椭圆上一动点, 求|PB|最大值.
(23) 已知点P(a,0)(a∈R),M是双曲线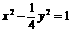 上的动点, 求|PM|的最小值.
上的动点, 求|PM|的最小值.
(24) 已知点P是抛物线y2=4px(p>0)上动点,Q(1, 0), 求|PQ|的最小值.
1. 二次函数法(用换元法化为二次函数)
求下列函数的值域
(1)
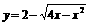
(2)
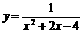
(3)
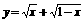
(4)
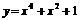
(5)
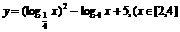 )
)
(6)
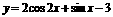
(7)
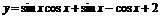
(8)
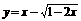
(9)
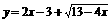
(10) 已知函数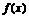 的值域是
的值域是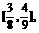 ,求函数
,求函数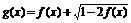 的值域.
的值域.
(11) 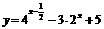 ,
,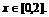
(12) 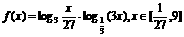
(13) 若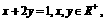 求函数
求函数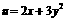 的取值范围.
的取值范围.
(14) 若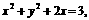 求函数
求函数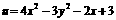 的值域.
的值域.
2.3 方程、不等式的同解原理本质上是保持方程和不等式中的函数的定义域在变形中不变
(1) 解不等式 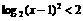
(2)
比较大小: 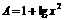 与
与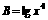
(3)
求函数f(x)=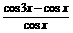 的最值.
的最值.
(4)
求函数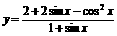 的值域.
的值域.
(5)
考察函数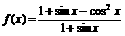 的奇偶性.
的奇偶性.
第三讲 函数的值域和最值
知识点及方法 二次函数法;函数单调性法;反解法(反函数法);数形结合法;均值不等式法
2.2 在求条件值域、最值中,注意条件关系式中变量的范围
(1) 已知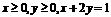 求
求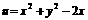 的取值范围.
的取值范围.
(2) 已知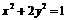 ,求
,求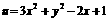 的取值范围.
的取值范围.
(3) 已知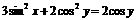 ,求
,求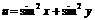 的取值范围.
的取值范围.
(4) 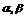 是方程
是方程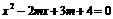 的两个实根,求
的两个实根,求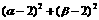 的取值范围.
的取值范围.
2.1换元法引起的变量范围即函数定义域的变化
(1) 求函数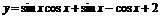 的值域.
的值域.
(2) 求函数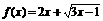 的值域.
的值域.
(3) 求函数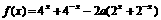 的值域
的值域
(4) 若方程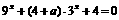 有解,求实数
有解,求实数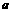 的取值范围.
的取值范围.
(5) 若方程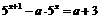 有负根,求实数
有负根,求实数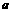 的取值范围.
的取值范围.
(6) 若方程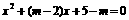 的两根都大于2,求
的两根都大于2,求 的取值范围.
的取值范围.
(7) 若方程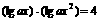 的所有解都大于1,求
的所有解都大于1,求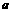 的取值范围.
的取值范围.
2. 定义域的“隐藏”性
1.求函数的定义域
(1)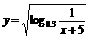
(2) 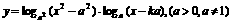
(3) 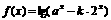
(4) 设函数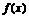 的定义域是[0,1],求
的定义域是[0,1],求 的定义域.
的定义域.
(5) 设函数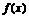 的定义域是[0,2],
求
的定义域是[0,2],
求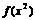 的定义域.
的定义域.
(6) 设函数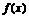 的定义域是
的定义域是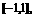 求函数
求函数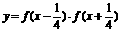 的定义域.
的定义域.
(7) 设函数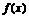 的定义域是[
的定义域是[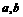 ],
],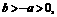 求函数
求函数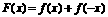 的定义域.
的定义域.
(8) 设函数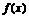 的定义域是
的定义域是 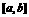 ,
,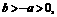 求函数
求函数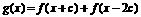 的定义域.
的定义域.
(9) 设函数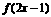 的定义域是[0,1],
求函数
的定义域是[0,1],
求函数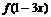 的定义域.
的定义域.
5. 用补集思想解题
(1)
已知函数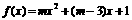 的图象与x轴的交点至少有一个在原点左侧,求实数m的取值范围.
的图象与x轴的交点至少有一个在原点左侧,求实数m的取值范围.
(2) 从5本中文书和6本英文书中任取3本,其中至少有一本英文书的取法种数是多少?
(3) 从8名男生和4名女生中选出5名学生参加数学竞赛,至少有两名女生的取法种数是多少?
第二讲 函数的定义域
知识点及方法求函数的定义域;定义域在函数、方程、不等式中的应用
4. 方程、不等式与集合
(1) 已知方程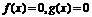 的解集分别为
的解集分别为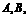
写出方程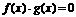 的解集
的解集
写出方程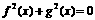 的解集
的解集
写出方程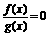 的解集
的解集
(2) 已知不等式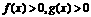 的解集分别为
的解集分别为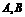
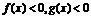 的解集分别为
的解集分别为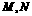 写出不等式
写出不等式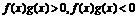 的解集.
的解集.
(3)
设全集为R,记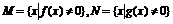 ,试写出
,试写出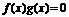 的解集.
的解集.
(4)
已知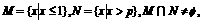 求p的取值范围
求p的取值范围
(5)
设集合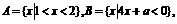 若
若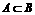 ,求a的取值范围.
,求a的取值范围.
(6)
已知集合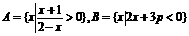 ,且
,且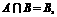 求p的取值范围.
求p的取值范围.
(7)
已知集合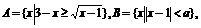 且
且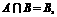 求a的取值范围.
求a的取值范围.
(8)
已知集合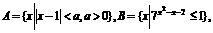 且
且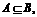 求A的取值范围.
求A的取值范围.
(9)
已知集合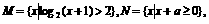 且
且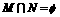 ,求a的取值范围.
,求a的取值范围.
(10) 已知 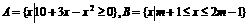 ,且
,且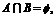 求m的取值范围.
求m的取值范围.
(11) 已知集合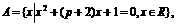 且
且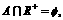 求p的取值范围.
求p的取值范围.
(12) 设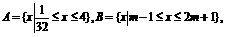 若
若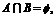 求m的取值范围.
求m的取值范围.
(13) 已知函数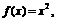 集合
集合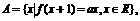 且
且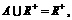 求a的取值范围.
求a的取值范围.
(14) 已知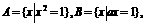 若
若 求a的值.
求a的值.
(15) 已知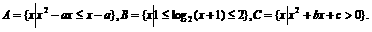 ①若
①若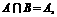 求a的取值范围.②若
求a的取值范围.②若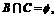 且
且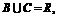 求b,c的值.
求b,c的值.
(16) 集合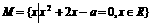 ,若
,若 求a的取值范围.
求a的取值范围.
(17) 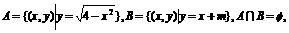 求实数m的取值范围.
求实数m的取值范围.
(18) 已知集合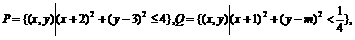 且
且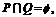 求m的取值范围.
求m的取值范围.
4. 集合与充要条件
判断充要条件关系
(1) x>0 是 x2>0
(2) x2=1 是 x=1
(3) lgf(x)>lgg(x) 是 f(x)>g(x)
(4) 0<x<5 是 ∣x-2∣<3
(5) 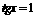 是
是 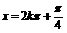 ,
,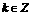
(6) 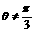 是
是 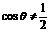
(7) 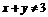 是
是
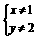
(8) 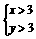 是
是 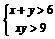
(9) 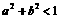 是
是
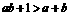
(10) 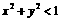 是
是 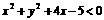
(11) 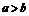 是
是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com