
题目列表(包括答案和解析)
3.提出虚数、纯虚数、实部与虚部等复数的有关概念
在学生掌握复数的代数形式的基础上,提出复数的有关概念是顺理成章的事.教学中注意渗透数学中的重要思想方法--分类与讨论思想,同时结合以下实例加深对复数有关概念的理解.
例1 下列数中,哪些是实数,哪些是虚数,哪些是纯虚数?并分别指出这些复数的实部与虚部各是什么.
3,-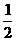 -
-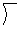 2,0,-
2,0,-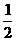
例2 t取何实数时,复数z=(t2-1)+(t-1)I是
(1)零? (2)纯虚数?,(3)虚数?
4,提出两个复数相等的定义与虚部分别对应相等.也就是1)十(‘-1)i是
(3)虚数?
即两个复数相等的充要条件是它们的实部 O十6f二c+df㈡d二c,且占二d 由此容易得出:。+执’0㈡o’0,且A二0.
这是复数这一章中最重要的基础知识之一要依据.
它是求复数值及在复数集C中解方程的重
这里顺便说明,两个复数只能说相等或不相等,而不能比较大小.教科书中举例说1+i与3+5i不能比较大小,学生不易接受.教学中,可说明i与2i不能比较大小,以帮助学生初步了解,为什么说两个不全为实数的复数不能比较大小.
2.提出复数的代数形式的概念
在复习提问(2)的基础上,由i的第二条性质提出复数的代数形式的概念明如下两点:
(1)复数的代数形式a+bi是复数的表示形式之一;
(2)任何一个复数a+bi,必须由一个有序实数对(a,b)唯一确定第(2)点说明可为后续学习打下基础.
这时必须说
1.复习提问
(1)简要说明引进新数i的必要性.
(2)引入新数i后,对它有哪两点规定?
2.理解复数相等的定义,并会应用它来解决有关问题.
1.掌握复数的代数形式,理解虚数、纯虚数、实部与虚部等有关复数的概念
10.归纳总结
由于复数代数形式的加减法相对来说容易被学生理解和接受,这里教师着重对复数加减法的几何意义进行小结。
布置作业:
教科书习题5.3第2、3、4、5题。
9.课堂练习
教科书课后练习第2、5题。
8. 讲解例2
讲解例2
例2


 根据复数的几何意义及向量表示,求复平面内圆的方程。
根据复数的几何意义及向量表示,求复平面内圆的方程。
分析:平面内到一定点的距离等于常数的动点的轨迹是圆。根据
复平面内两点的距离公式可得到的方程。
解:如图5-7,设复平面内⊙P的圆心P 与复数P =a+bi对应,
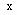
 圆的半径为r,圆上任意一点Z与复数Z =x+yi对应,则
圆的半径为r,圆上任意一点Z与复数Z =x+yi对应,则 
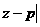 =r。这就是复数平面内的圆的方程。特别地,当圆心P 在原点时,圆的方程就成了
=r。这就是复数平面内的圆的方程。特别地,当圆心P 在原点时,圆的方程就成了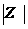
 =r.把他们转化成
=r.把他们转化成
实数方程,就是 Z P
(x-a)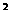 +(y-b)
+(y-b)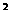 =r
=r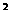
x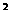 +y
+y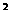 = r
= r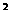
这就是几何中的标准方程。从方程形式来看,圆的复数方程要比他相应的实数方程简捷得多。
6.课堂练习
 教科书中的课后练习第3、4题。
教科书中的课后练习第3、4题。

 7.研究复数加减法的几何意义
7.研究复数加减法的几何意义

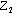
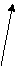
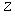
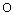
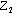

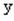
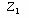
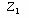
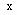
 复数加减法的几何意义是本节课的难点,教学中,应充分利用学生已有的向量知识基础来突破这一难点。
复数加减法的几何意义是本节课的难点,教学中,应充分利用学生已有的向量知识基础来突破这一难点。
设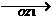 及
及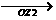 分别与复数a+bi 及c+di对应,且
分别与复数a+bi 及c+di对应,且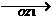 、
、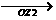 不共线(图5-6(甲)),以
不共线(图5-6(甲)),以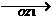 及
及
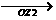 为两条邻边画平行四边形OZ1ZZ2,可问学生对角线OZ所表示的向量
为两条邻边画平行四边形OZ1ZZ2,可问学生对角线OZ所表示的向量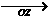 对应的复数是什么。然后,指出这就是复数加法的几何意义。
对应的复数是什么。然后,指出这就是复数加法的几何意义。
讲复数减法的几何意义时,应结合复数减法是复数加法的逆运算、复数加法的几何意义及图5-6(乙)来进行。
如图5-6(乙),由向量知识有:
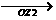 +
+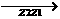 =
=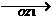
这正好与(c+di)+(x+yi)=a+bi对应.作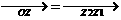 ,则向量
,则向量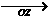 (即
(即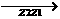 )对应复数
)对应复数
这样,就得到了复数减法的几何意义.
设Z1Z2两点间的距离为d,则
d=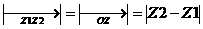
=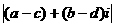
=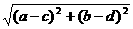 .
.
这就是复平面内两点间的距离公式,它与平面的直角坐标系中两点间的距离公式是一致的.
5.讲解例1
例1 计算(5-6I)+(-2-I)-(3+4I).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com