
题目列表(包括答案和解析)
37、已知动圆与圆F1:x2+y2+6x+4=0和圆F2:x2+y2-6x-36=0都外切。
(I)求动圆圆心的轨迹C的方程;
(II)若直线l被轨迹C所截得的线段的中点坐标为(-20,-16),求直线l的方程;
(Ⅲ)若点P在直线l上,且过点P的椭圆C∕以轨迹C的焦点为焦点,试求点P在什么位置时,椭圆C∕的长轴最短,并求出这个具有最短长轴的椭圆C∕的方程。
36、已知:f(x)=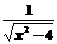 (x<-2),f(x)的反函数为g(x),点An(an,
(x<-2),f(x)的反函数为g(x),点An(an,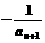 )在曲线y=g(x)上(n∈
)在曲线y=g(x)上(n∈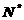 ),且a1=1.
),且a1=1.
(I)求y=g(x)的表达式;
(II)证明数列{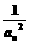 }为等差数列;
}为等差数列;
(Ⅲ)求数列{an}的通项公式;
(Ⅳ)设bn=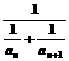 ,记Sn=b1+b2+……+bn,求Sn.
,记Sn=b1+b2+……+bn,求Sn.
35、已知函数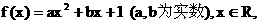
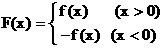
(1)若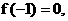 且函数
且函数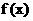 的值域为
的值域为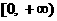 ,求
,求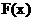 的表达式;
的表达式;
(2)在(1)的条件下,
当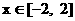 时,
时, 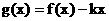 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设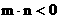 ,
, 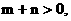
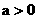 且
且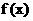 为偶函数, 判断
为偶函数, 判断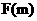 +
+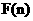 能否大于零?
能否大于零?
34、(本小题满分14分)
椭圆E的中心在原点O,焦点在x轴上,离心率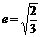 ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: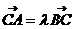 (λ≥2)。
(λ≥2)。
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程。
33、(本小题满分12分)
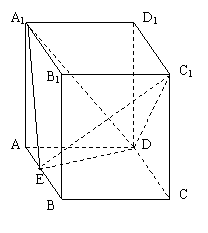 如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
(I)求证:平面A1ED⊥平面ABB1A1;
(II)求二面角A1-ED-C1的余弦值;
(III)求点C1到平面A1ED的距离。
32、(本小题满分12分)
设事件A发生的概率为P,若在A发生的条件下B发生的概率为P/,则由A产生B的概率为PP/,根据这一规律解答下题:一种掷硬币走跳棋的游戏:棋盘上有第0,1,2,3,…,100,共101站,设棋子跳到第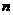 站的概率为
站的概率为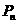 ,一枚棋子开始在第0站(即
,一枚棋子开始在第0站(即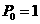 ),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为
),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为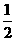 。
。
⑴ 求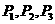 ,并根据棋子跳到第
,并根据棋子跳到第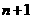 站的情况,试用
站的情况,试用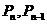 表示
表示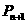 ;
;
⑵ 设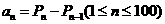 ,求证:数列
,求证:数列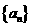 是等比数列,并求出
是等比数列,并求出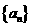 的通项公式;
的通项公式;
⑶ 求玩该游戏获胜的概率
30、已知向量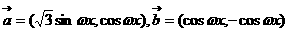 ,ω>0,记函数
,ω>0,记函数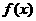 =
=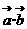 ,已知
,已知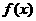 的最小正周期为
的最小正周期为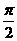 .
.
⑴ 求ω的值;
⑵ 设△ABC的三边a、b、c满足b2=ac,且边b所对的角为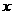 ,
,
求此时函数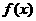 的值域。
的值域。
29、若平移椭圆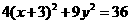 ,使平移后的椭圆的中心在第一象限,且它与
,使平移后的椭圆的中心在第一象限,且它与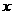 轴、
轴、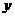 轴分别只有一个交点,则平移后的椭圆方程是____________________
轴分别只有一个交点,则平移后的椭圆方程是____________________
28、已知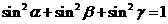 (
(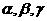 为锐角),那么
为锐角),那么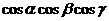 的最大值为________________________
的最大值为________________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com