
题目列表(包括答案和解析)
5.解(1)[法一]由A(-2,1),B(-4,-1)得直线AB即直线MN方程为y=x+3,代入椭圆C1的方程并整理,得(a2+b2)x2+6a2x+9a2-a2b2=0 (*)
设M(x1,y1),N(x2,y2),则 x1+x2=-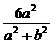
∵A(-2,1)是弦MN的中点,∴x1+x2=-4,故由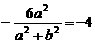 得a2=2b2,
得a2=2b2,
又b2=a2-c2,∴a=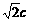 ,从而椭圆离心率e1=
,从而椭圆离心率e1=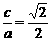 .
.
∵A为C2的焦点,且相应准线l方程为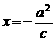 ,即
,即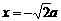 ,过B作BB0⊥l于B0,则由双曲线定义知,e2=
,过B作BB0⊥l于B0,则由双曲线定义知,e2=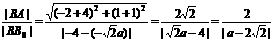 .
.
法二:设M(x1,y1),N(x2,y2),则x1+x2=4,y1+y2=2,且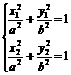
 ,
,
4. 解:(1)因为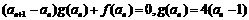
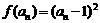 所以
所以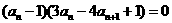 ,又
,又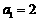 ,所以
,所以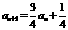
(2)因为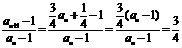
所以,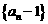 是以
是以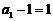 为首项,公比为
为首项,公比为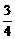 的等比数列.
的等比数列.
(3)由(2)可知,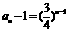 , 所以
, 所以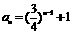 ,
,
从而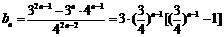 .
.
因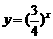 为减函数,所以bn中最大项为b1=0. 又bn=
为减函数,所以bn中最大项为b1=0. 又bn=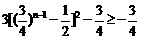 ,
,
而此时n不为整数才能有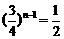 ,所以只须考虑
,所以只须考虑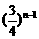 接近于
接近于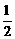 .
.
当n=3时,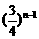 =
=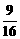 与
与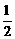 相差
相差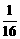 ;当n=4时,
;当n=4时,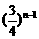 =
=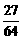 与
与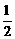 相差
相差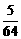 ,
,
而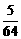 >
>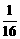 ,所以bn中项
,所以bn中项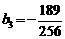 .
.
3. 证:(1)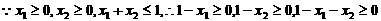
要证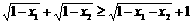 ,
,
只要让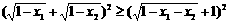
即证: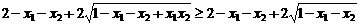
只要证: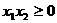
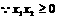 成立,故原不等式也成立。
成立,故原不等式也成立。
解(2)从(1)的证明过程可知当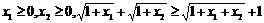 成立
成立
,等号当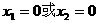 时取到.
时取到.
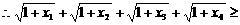
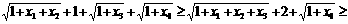
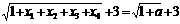
等号当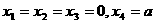 取到。
取到。
2. (1)证明 函数定义域为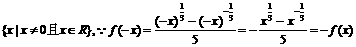
∴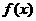 为奇函数.
为奇函数.
设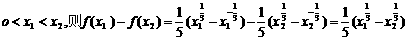
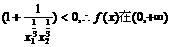 上是增函数,又
上是增函数,又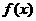 是奇函数.
是奇函数.
∴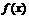 在(-∞,0)上也是增函数.
在(-∞,0)上也是增函数.
(2)解 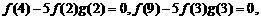 猜想:
猜想: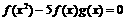
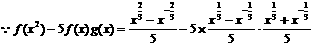
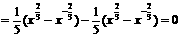
1. (1)椭圆C的方程为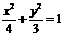 ,焦点F1(-1,0)、F2(1,0);
,焦点F1(-1,0)、F2(1,0);
(2)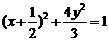 ;(3)定值为
;(3)定值为 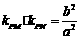
1. 9002. 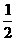 3. 1023 4. 1 5.
3. 1023 4. 1 5. 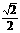 6. ①③④7. ①②③④⑤8. 4
6. ①③④7. ①②③④⑤8. 4
1. C2. C3. D4. A5. B6. D7. B8. D9. D10. B11. B12.A13.D14.A15.C16. C17. D18. B19. A20. B21. B22. B23. C
12. 已知二次函数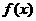 的二次项系数为负,对任意实数x都有
的二次项系数为负,对任意实数x都有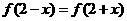 ,问当
,问当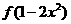 与
与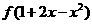 满足什么条件时才有-2<x<0?
满足什么条件时才有-2<x<0?
题型示例答案
11. △ABC中,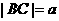 ,
,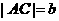 ,a,b是方程
,a,b是方程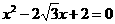 的两根,且2cos(A+B)=1.求:
的两根,且2cos(A+B)=1.求:
(1)角C的度数;(2)AB的长;(3)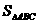
10. 在平面直角坐标系中,已知平行四边形ABCD,O为原点,且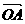 =a,
=a,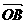 =b,
=b,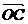 =c,
=c,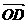 =d,E在BA上,且BE∶EA=1∶3,F在BD上,且BF∶FD=1∶4,用a,b,c,d分别表示
=d,E在BA上,且BE∶EA=1∶3,F在BD上,且BF∶FD=1∶4,用a,b,c,d分别表示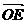 、
、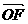 、
、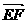 、
、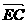 ,并判断E、F、C三点是否共线.
,并判断E、F、C三点是否共线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com