
题目列表(包括答案和解析)
22. (本题14分)已知数列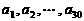 ,其中
,其中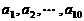 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;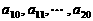 是公差为
是公差为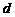 的等差数列;
的等差数列;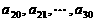 是公差为
是公差为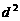 的等差数列(
的等差数列(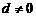 ).
).
(1)若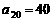 ,求
,求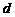 ;
;
(2)试写出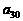 关于
关于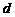 的关系式,并求
的关系式,并求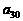 的取值范围;
的取值范围;
(3)续写已知数列,使得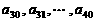 是公差为
是公差为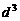 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
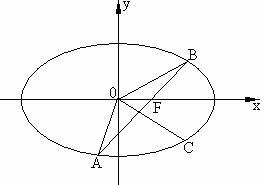
21. (本题12分) 如图 ,椭圆的中心在原点, 焦点在x轴上, 过其右焦点F作斜率为1的直线, 交椭圆于A、B两点, 若椭圆上存在一点C, 使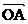 +
+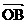 =
=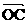 .
.
(1) 求椭圆的离心率;
 (2) 若
(2) 若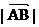 =15, 求这个椭圆的方程.
=15, 求这个椭圆的方程.
20.(本题12分)设函数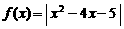 .
.
(1)在区间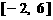 上画出函数
上画出函数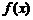 的图像;
的图像;
 (2)设集合
(2)设集合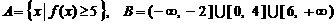 . 试判断集合
. 试判断集合 和
和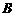 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当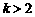 时,求证:在区间
时,求证:在区间 上,
上,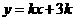 的图像位于函数
的图像位于函数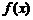 图像的上方.
图像的上方.
19. (本题12分) 如图, 在三棱S-ABC中, △ABC是边长为8的正三角形, SA=SC=2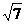 , 二面
, 二面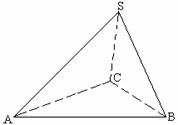 角S-AC-B为60°.
角S-AC-B为60°.
(1) 求证: AC⊥SB;
(2) 求二面角S-BC-A的正切值.
18. (本题12分) 已知向量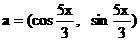 ,
,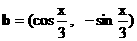 ,
, 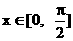 .
.
(1) 求a·b及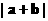 ;
;
(2) 若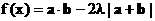 (其中
(其中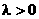 )的最小值是
)的最小值是 , 求
, 求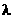 的值.
的值.
的文字说明、推理过程或计算步骤)。
17.(本题12分)已知数列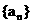 为等差列,
为等差列,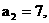
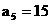 .
.
(1) 求数列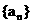 的通项公式;
的通项公式;
(2) 设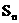 是数列
是数列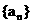 的前n项和,请比较
的前n项和,请比较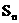 ·
·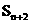 与
与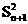 的大小.
的大小.
15. ; 16. ;
13. ; 14. ;
16. 已知数列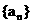 满足
满足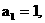
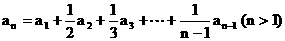 , 若
, 若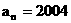 ,则
,则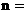 .
.
高三数学期末综合练习(六)
班级 姓名 学号 得分
15. 给出下列四个命题:
①若直线l⊥平面α,l//平面β,则α⊥β;
②各侧面都是正方形的棱柱一定是正棱柱;
③一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面,则这两个二面角的平面角互为补角;
④过空间任意一点一定可以做一个和两个异面直线都平行的平面。
其中,正确的命题的是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com