1、棱柱的定义、分类；　　 2、棱柱的主要性质；　　　　 3、平行六面体与长方体；

8、在棱长为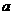的正方体ABCD－A₁B₁C₁D₁中，E、F、G分别是AA₁、BC、CC₁的中点，求顶点B₁到平面EFG的距离．

高三数学教学案　　　　 　　 　　第九章 立体几何

　第十六课时 棱柱、棱锥的概念与性质

考纲摘录

了解棱柱、棱锥的概念；掌握棱柱、棱锥的性质，会画直棱柱，正棱锥的直观图．

知识概要

7、已知正三角形ABC的边长为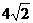，PA⊥平面ABC，PA=2，D、E、F分别是BC、DC、AC的中点，求直线AD到平面PEF的距离．

6、正三棱柱ABC－A₁B₁C₁的所有棱长都为1，M、M₁分别为棱BC、B₁C₁的中点，求直线AM与平面A₁M₁C的距离．

5、将半径为R的四个球，两两相切地放在桌面上，则上面的一个球的球心到桌面的距离为__________．

4、四棱柱ABCD－A₁B₁C₁D₁的底面ABCD为正方形，侧棱与底面边长均为2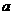，且∠A₁AD=∠A₁AB=60°，则侧棱AA₁和截面B₁D₁DB的距离是__________．

3、在四面体P－ABC，PA、PB、PC两两垂直，M是面ABC内一点且点M到三个面PAB、PBC、PCA的距离分别是2、3、6，则点M到顶点P的距离是(　 )

　　 A．7　　　　　　　　　　 B．8　　　　　　　　　　 C．9　　　　　　　　　　　　　　 D．10

2、平面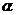内有∠XOY=60°，OA是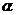的斜线且OA=10，∠AOX=∠AOY= 60°，则A到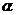的距离是__________．

1、△ABC中，AB=9，AC=15，∠BAC=120°，△ABC所在平面外一点P到三个顶点A、B、C的距离都是14，那么点P到平面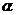的距离(　 )

　　　 A．7　　　　　　　　　　 B．9　　　　　　　　　　 C．11　　　　　　　　　　　　　 D．13

5、直三棱柱ABC－A₁B₁C₁中，∠ACB=90°，AC=AA₁=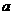，则点A到平面A₁BC的距离是___________．

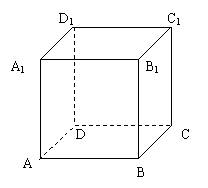例题讲解

例1、在棱长为1的正方体ABCD－A₁B₁C₁D₁中

(1)求点A到平面BD₁的距离；

(2)求点A₁到平面AB₁D₁的距离；

(3)求平面AB₁D₁与平面BC₁D的距离；

(4)求直线AB到平面CDA₁B₁的距离．

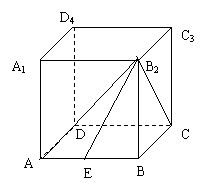例2、棱长为4的正方体ABCD－A₁B₁C₁D₁中，P、Q分别为棱CD、CD₁的中点，求P到平面A₁QC₁的距离．

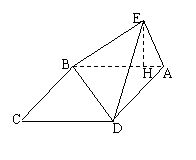例3、如图，在矩形ABCD中，AB=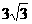，BC=3，沿对角线BD将△BDC折起，使点C移到点E，且点E在平面ABD上的射影H恰在AB上．

(1)求证：BE⊥平面ADE；

(2)求点A到平面BDE的距离．

课后作业

班级_______学号__________姓名_________