
题目列表(包括答案和解析)
1、如果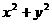 =1,则
=1,则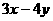 的最大值是___________.
的最大值是___________.
4、设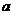 、
、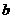 、
、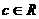 ,
,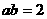 且
且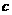 ≤
≤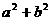 恒成立,则
恒成立,则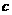 的最大值是_______________.
的最大值是_______________.
例题讲解
例1、已知1≤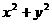 ≤2,求证:
≤2,求证: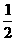 ≤
≤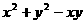 ≤3.
≤3.
例2、求证:(1)2(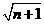 -1)<
-1)<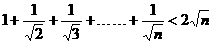
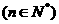
(2)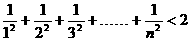
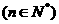
例3、已知a、b∈R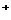 ,a+b=1,求证:
,a+b=1,求证: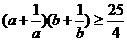 .
.
例4、设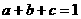 ,
,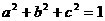 ,且
,且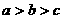 .求证:
.求证: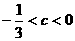 .
.
课后练习
班级_______学号__________姓名_________
3、设实数 、
、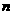 、
、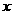 、
、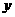 满足
满足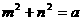 ,
,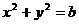 (
(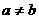 )则
)则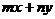 的最大值是__________.
的最大值是__________.
2、实数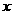 、
、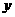 满足
满足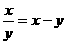 ,则
,则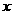 的取值范围是
( )
的取值范围是
( )
A.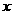 <0 B.
<0 B.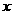 ≥4 C.
≥4 C.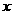 ≤0或
≤0或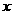 ≥4 D.
≥4 D.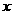 <0或
<0或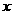 ≥4
≥4
1、设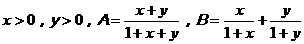 ,则
,则 与
与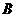 的大小关系是_______.
的大小关系是_______.
10、(选做题)是否存在常数c,使得不等式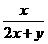 +
+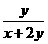 ≤c≤
≤c≤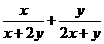 对任意正数x、y恒成立?试证明你的结论。
对任意正数x、y恒成立?试证明你的结论。
高三数学教学案 第六章 不等式
班级_______学号__________姓名_________
第六课时 不等式的证明(三)
考纲摘录
了解用放缩法、换元法、判别式法等方法证明简单的不等式.
知识概要
放缩法:利用不等式的传递性,对不等式进行放大或缩小,主要放缩的方法有:增项、减项、利用分式的性质、利用不等式的性质、利用函数的性质等。
换元法:主要是三角换元法与增量换元法,注意换元后新变量的取值范围.
判别式法:根据已知或构造出的一元二次方程、一元二次不等式、一元二次函数的根、解集、函数的性质等特征确定出其判别式所应满足的不等式,从而推出欲证的不等式的方法.
基础训练
9、(1)已知|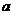 |<1,|
|<1,|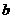 |<1,求证:
|<1,求证: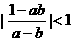 .
.
(2)求实数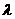 的取值范围,使不等式
的取值范围,使不等式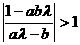 对一切实数
对一切实数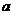 、
、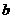 恒成立,其中
恒成立,其中
|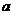 |<1,|
|<1,|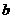 |<1.
|<1.
8、已知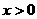 ,
,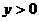 ,且
,且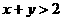 ,则
,则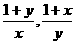 中至少有一个小于2.
中至少有一个小于2.
7、若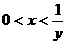 ,求证:
,求证: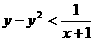 .
.
6、已知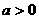 ,
,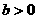 ,2
,2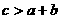 .求证:
.求证: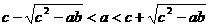 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com