1、用等可能性事件的概率公式P(A)=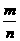解题时，一定先弄清该事件的“一次试验”是什么，再看确定的基本事件相互间是否等可能性。

3、能熟练地运用排列组合的知识解决等可能性事件的概率问题。

重点、难点

2、掌握等可能性事件的概率公式P(A)=。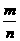

1、了解随机事件、必然事件、不可能事件的概念。

8、(附加题)

质点A位于数轴x=0，质点B位于x=2处，这两个质点每隔1秒就向左或向右移动1

个单位，设向左移动的概率为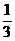，向右移动的概率为。

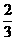(1)求3秒末，质点A在x=1处的概率；

(2)求2秒末，质点A、B同时在x=2处的概率；

(3)假若质点c在x=0，x=1两处之间移动，并满足：当质点C在x=0处时，1秒末

必移到x=1处；当质点c在x=1处，1秒末必分别以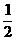的概率停留在x=1处或移动到x=0处，今质点c在x=1处，求8秒末质点c在x=1处的概率。

7、学校举行了演讲比赛，某班计划从4名女生和2名男生中任选3人参加，求：

(1)所选3人都是女生的概率；

(2)所选3人中恰有1名男生的概率；

(3)所选3人中至少有一名男生的概率。

6、某次1500米体能测试中，甲、乙、丙三人各自通

过测试的概率分别为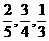，求：

(1)3人都通过体能测试的概率；

(2)只有2人通过体能测试的概率。

5、如图是15 0辆汽车通过某路段时速度的频率

分布直示图，

则速度在[60，70)的汽车大约有(　　 )

A　 100辆　　　 B　 80辆　　　

C　 60辆　　 　　D　 45辆

4、已知一组样本x₁，x₂，…x_n的平均值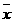=5，方差S²=4，则样本2x₁+3，2x₂+3,…2x_n+3

的均值和方差分别为________、_________。

3、对总数为N的一批零件抽取一个容量为40的样本，若对每个零件被抽取的概率为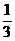

则N的值为(　　 )

A　 200　　　　 B　 150　　　　 C　 120　　　　 D　 100