
题目列表(包括答案和解析)
8、甲、乙两个篮球运动员,投篮命中率分别是0.7和0.8,每人投篮两次。
(1)求甲进2球,乙进1球的概率;
(2)若投进1球得2分,未投进得0分,求甲、乙二人得分相等的概率。
高三数学教学案 第十章 排列、组合与概率
第十课时 概率与统计
考纲摘录
7、从1、2、3、4、5五个数字中,任意有放回地连续抽取三个数字,求下列事件的概率:
(1)三个数字完全不同;(2)三个数字中不含1和5;(3)三个数字中5恰好出现两次。
6、某射手射击1次,击中目标的概率是0.9,他连续射击4次,且他各次射击是否击中目标相互之间没有影响,有下列结论:
(1)他第3次击中目标的概率是0.9;
(2)他恰好击中目标3次的概率是0.9×0.1;
(3)他至少击中目标1次的概率是1-0.14。
其中正确结论的序号是__________。(写出所有正确结论的序号)
5、有10名学生,其中4名男生,6名女生,从中任选2名学生,恰好是2名男生或2名女生的概率是( )
A 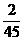 B
B 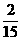 C
C 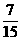 D
D 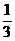
4、用5门命中率均为0.6的高射炮同时射击一架敌机,至少有一门击中敌机的概率为_______.(保留两个有效数字)
3、在含有4件次品的100件产品中,每次取1件,取后放回,连取4次,所取的4件产品中恰有1件次品的概率为_________。(保留两个有效数字)
2、一射手命中10环的概率为0.7,命中9环的概率为0.3,求该射手三发命中不少于29环的概率为_________。
1、把一枚硬币连掷5次,恰好出现2次反面的概率为__________。
5、一射手对同一目标独立地射击四次,已知至少命中一次的概率为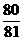 ,则此射手每次射击命中的概率为 ( )
,则此射手每次射击命中的概率为 ( )
A 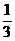 B
B 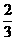 C
C 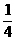 D
D 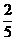
例题讲解
例1:盒中6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品; (2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品
例2:如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作,已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90,分别求两个系统N1,N2正常工作的概率P1,P2。
 A B C
A B C
N1
|
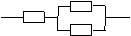 A B
A B
N2
例3:甲、乙两名围棋手进行比赛,已知每一局甲获胜的概率是0.6,乙获胜的概率是0.4,比赛时可采用三局两胜或五局三胜制,问在哪一种比赛制度下,甲获胜的可能性较大。
例4:将一枚硬币连续抛掷15次,(1)若该硬币均匀(出现正、反面的概率相等),求正面向上为奇数次的概率,并说明正面向上为奇数次的概率与正面向上为偶数次的概率是否相等。(2)若该硬币有暇疵,正面向上的概率为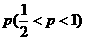 ,说明正面向上为奇数次的概率与正面向上为偶数次的概率是否相等。
,说明正面向上为奇数次的概率与正面向上为偶数次的概率是否相等。
课后作业
班级_______学号__________姓名_________
4、种植两株不同的花卉,它们的存活率分别为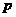 、q,则恰有一株存活的概率为( )
、q,则恰有一株存活的概率为( )
A P+q-2pq B P+q-pq C p+q D pq
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com