
题目列表(包括答案和解析)
4. 复数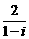 的值为
的值为
3.直线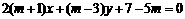 与直线
与直线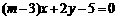 垂直的充要条件是
垂直的充要条件是
2. 等差数列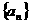 中,
中,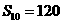 ,那么
,那么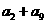 的值是
的值是
1.已知全集U=R,集合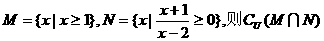
21.解:(I)由题意知,曲线C3向左平移我个单位得到曲线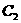 ,
,
 曲线
曲线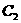 是函数
是函数 的图象 …………………………2分
的图象 …………………………2分
曲线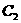 与曲线
与曲线 关于直线
关于直线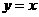 对称,
对称,
 曲线C1是函数
曲线C1是函数 的反函数的图象
的反函数的图象
∵ 的反函数为
的反函数为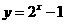
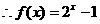 ………………………………………………………4分
………………………………………………………4分
(Ⅱ)由题设: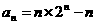 ,
,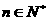
∴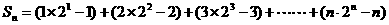
 ……6分
……6分

即 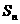
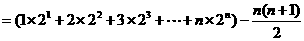 ①
①
∴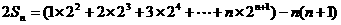 ②
②
由②-①得 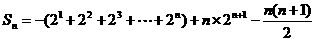

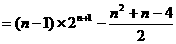 ……………………8分
……………………8分
当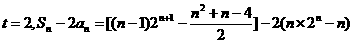

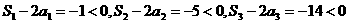
当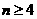 时,
时,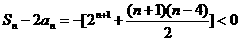
 当
当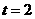 时,对一切
时,对一切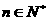 ,
,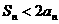 恒成立 ………………11分
恒成立 ………………11分
当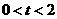 时,
时, 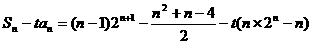

记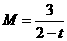 ,则当
,则当 大于比
大于比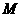 大的正整数时,
大的正整数时,

这就证明当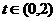 时,存在正整数
时,存在正整数 ,使得
,使得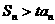 .
.
也就是说当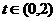 时,
时, 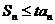 不可能对一切
不可能对一切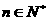 都成立.
都成立.
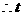 的最小值为
的最小值为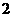 . …………………………14分
. …………………………14分
21.(本小题满分14分,第一小问满分4分,第二小问满分10分)
设函数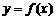 的图象是曲线C1,曲线C2与C1关于直线
的图象是曲线C1,曲线C2与C1关于直线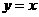 对称。将曲线C2向右平移1个单位得到曲线C3,已知曲线C3是函数
对称。将曲线C2向右平移1个单位得到曲线C3,已知曲线C3是函数 的图象。
的图象。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)设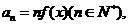 求数列
求数列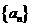 的前
的前 项和
项和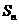 ,并求最小的正实数
,并求最小的正实数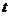 ,使
,使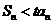 对任意
对任意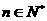 都成立。
都成立。
20.(Ⅰ)解: ,
,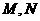 是直线
是直线 与双曲线两条渐近线的交点,
与双曲线两条渐近线的交点,
 ,
即
,
即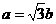 ………………2分
………………2分
 双曲线的焦距为4,
双曲线的焦距为4,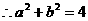 ……………………4分
……………………4分
解得,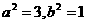
 椭圆方程为
椭圆方程为 …………5分
…………5分
(Ⅱ)解:设椭圆的焦距为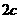 ,则点
,则点 的坐标为
的坐标为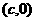
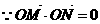 ,
, 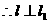
 直线
直线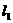 的斜率为
的斜率为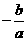 ,
, 直线
直线 的斜率为
的斜率为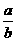 ,
,
 直线
直线 的方程为
的方程为 …………………………………………7分
…………………………………………7分
由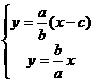 解得
解得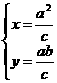 即点
即点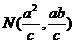
设 由
由 , 得
, 得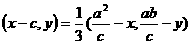
即
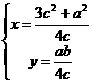
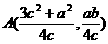 ……10分。
……10分。
 点
点 在椭圆上,
在椭圆上, ………………………………12分
………………………………12分
即 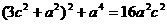 ,
,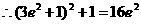
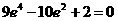


椭圆的离心率是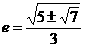 ……………………14分
……………………14分
20.(本小题满分14分,第一小问满分5分,第二小问满分9分)
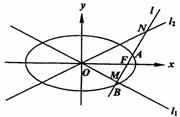
已知 为椭圆
为椭圆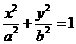
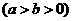 的右焦点,直线
的右焦点,直线 过点
过点 且与双曲线
且与双曲线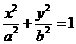 的两条渐进线
的两条渐进线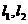 分别交于点
分别交于点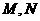 ,与椭圆交于点
,与椭圆交于点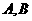 .
.
(Ⅰ)若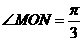 ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。
 (Ⅱ)若
(Ⅱ)若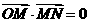 (
( 为坐标原点),
为坐标原点), ,求椭圆的离心率
,求椭圆的离心率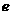 。
。
19.(Ⅰ)证明:
 在平面
在平面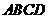 上的射影为O,
上的射影为O,
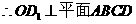 ,
, 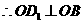 ……………………2分
……………………2分
 点
点 为
为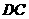 的中点,
的中点,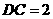 ,
, OC=1
OC=1
又 ,
,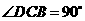 ,∠BOC=45°
,∠BOC=45°
同理∠AOD=45°, ∴∠AOB=90°。 ∴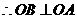 ……………………4分
……………………4分
 ,
, …………………………5分
…………………………5分
(Ⅱ)解法一: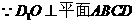 ,
,
又
 ,
, AD
AD 平面
平面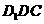
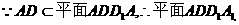
在平面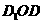 内,作
内,作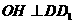 ,垂足为
,垂足为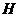 ,则
,则 。
。
∴线段 的长为点
的长为点 到平面
到平面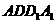 的距离……………………7分
的距离……………………7分

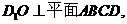
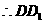 在平面
在平面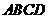 上的射影为
上的射影为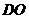 。
。
 为侧棱
为侧棱 与平面
与平面 所成的角.
所成的角.
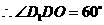 ……9分
……9分
在 中,
中,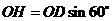 =
=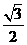 。
。
即点 到平面
到平面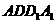 的距离为
的距离为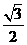 ……10分
……10分
解法二:∵D1O⊥平面ABCD,∴DD1在平面ABCD上的射影为DO
∴∠D1DO为棱DD1与平面ABCD所成的角, ∴∠D1DO=60° …………7分
∵OD=1, ∴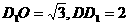
∴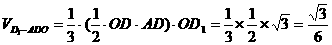
∵AD⊥DO,AD⊥D1O, ∴AD⊥平面D1DO ∴AD⊥DD1
设点O到平面ADD1A1的距离为h,
则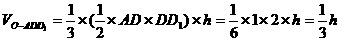 ………………9分
………………9分
∵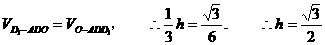
(Ⅲ)解:如图,作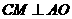 于
于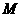 ,
,
作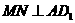 于
于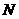 ,连结
,连结
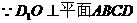 ,
,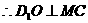
又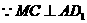 ,
,
又 ,
,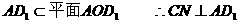
 为二面角
为二面角 的平面角,……………………13分
的平面角,……………………13分
在 中,
中,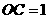 ,
,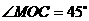 ,
,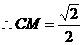 .
.
在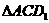 中,
中,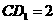 ,
,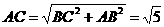 ,
,
取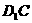 的中点
的中点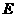 ,连结
,连结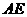 ,则
,则 ,
,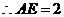
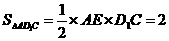
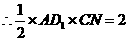 ,
,
在 中,
中,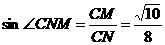
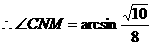 .
.
二面角 的大小为
的大小为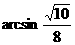 .………………………………16分
.………………………………16分
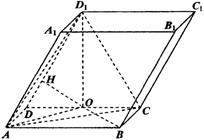
19.(本小题满分16分,第一小问满分5分,第二小问满分5分,第二小问满分6分)
如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD是矩形,AB=2,AD=1,顶点D1在底面ABCD上的射影O是CD的中点,侧棱与底面所成的角为60°。
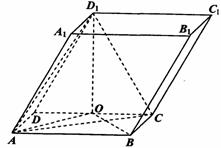 (Ⅰ)求证:
(Ⅰ)求证: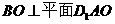 ;
;
(Ⅱ)求点O到平面AA1D1D的距离;
(Ⅲ)求二面角C-AD1-O的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com